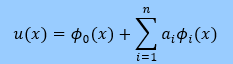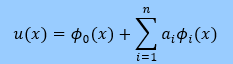One Dimensional Finite Element Method
Weighted Residual Method-14
■自由度n■
次のLinear Elementに行く前に計算精度の向上について述べておきます。
”もっと精度を向上できないか”というのが技術者の要望ですよね。
これまでに紹介した例題は自由度n=2が最高位でした。
しかもDirichlet境界-Dirichlet境界の問題のみでした。
Dirichlet境界-Neumann境界の問題はn=1でした。
自由度n=4までのプログラムを作成して精度が向上することを確認しましたので紹介しておきます。
φ2(x),
φ3(x),
φ4(x)の拡張方法について
1つの案を紹介します。
まず近似式は以下で変更ありません。
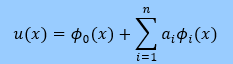 Dirichlet境界-Dirichlet境界の場合:
φ0(x)は以下でした。
これはそのまま使えます。
\begin{eqnarray}
\phi_0(x)=u(0)N_1(x)+u(L)N_2(x)
\end{eqnarray}
φi(x)はどうなるでしょう。
条件の
φi(0)=0と
φi(L)=0を満足しなければなりません。
条件を満たす以下が使えそうです。
つまりφ1(x)のi乗です。
\begin{eqnarray}
\phi_i(x)=\left(N_1(x)N_2(x)\right)^i
\end{eqnarray}
例題を上で示す
φi(x)を用いてプログラム作成と計算を行いました。
また自由度がn=2の場合の説明は
WRM6を見て下さい。
Dirichlet境界-Dirichlet境界の場合:
φ0(x)は以下でした。
これはそのまま使えます。
\begin{eqnarray}
\phi_0(x)=u(0)N_1(x)+u(L)N_2(x)
\end{eqnarray}
φi(x)はどうなるでしょう。
条件の
φi(0)=0と
φi(L)=0を満足しなければなりません。
条件を満たす以下が使えそうです。
つまりφ1(x)のi乗です。
\begin{eqnarray}
\phi_i(x)=\left(N_1(x)N_2(x)\right)^i
\end{eqnarray}
例題を上で示す
φi(x)を用いてプログラム作成と計算を行いました。
また自由度がn=2の場合の説明は
WRM6を見て下さい。
計算結果のu(0.5)と厳密解の絶対差を下のグラフに示します。
横軸は自由度のnです。
u(0.5)はDirichlet境界から一番遠い点ですから誤差が最大になると考えられる。
計算精度を高めるため領域の分割数をNSEG=10000にし、
微分も4次精度の中心差分で計算してあります。
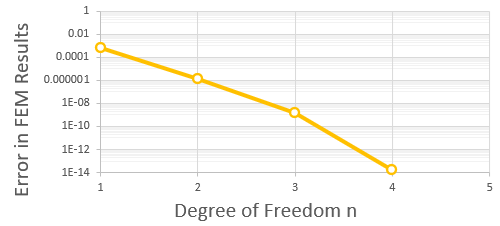 上の図を見るとn=4で誤差が倍精度(有効桁数=ほぼ14)の限界の1E-14のレベルまで達しています。
Dirichlet境界-Neumann境界の場合:
φ0(x)は下の2つ紹介しました。どちらも使えます。
これらのφ0(x)に関しては
WRM9を参考にして下さい。
\begin{eqnarray}
\phi_0(x)=u(0)+LSN_1(x)
\end{eqnarray}
\begin{eqnarray}
\phi_0(x)=u(0)-LSN_1(x)N_2(x)
\end{eqnarray}
φi(x)はどうなるかと言うと
φi(x)この条件をクリアーする必要があります。
左端境界はDirichletですので
φi(0)=0ですね。
φi(x)として以下が使えそうです。
これもφ1(x)のi乗です。
\begin{eqnarray}
\phi_i(x)=\left(N_1(x)N_2(x)+N_2(x)\right)^i
\end{eqnarray}
プログラム作成と計算を実施しましたので紹介します。計算条件はDirichlet-Dirichletと同じ
例題を使いました。ただし、領域はx=0からx=0.5で
x=0.5がNeumann境界のS=0です。
ですので未知数のu(0.5)は上で紹介したDirichlet-Dirichletと同じ値になるはずです。
下表にプログラムと計算結果を示します。
上の図を見るとn=4で誤差が倍精度(有効桁数=ほぼ14)の限界の1E-14のレベルまで達しています。
Dirichlet境界-Neumann境界の場合:
φ0(x)は下の2つ紹介しました。どちらも使えます。
これらのφ0(x)に関しては
WRM9を参考にして下さい。
\begin{eqnarray}
\phi_0(x)=u(0)+LSN_1(x)
\end{eqnarray}
\begin{eqnarray}
\phi_0(x)=u(0)-LSN_1(x)N_2(x)
\end{eqnarray}
φi(x)はどうなるかと言うと
φi(x)この条件をクリアーする必要があります。
左端境界はDirichletですので
φi(0)=0ですね。
φi(x)として以下が使えそうです。
これもφ1(x)のi乗です。
\begin{eqnarray}
\phi_i(x)=\left(N_1(x)N_2(x)+N_2(x)\right)^i
\end{eqnarray}
プログラム作成と計算を実施しましたので紹介します。計算条件はDirichlet-Dirichletと同じ
例題を使いました。ただし、領域はx=0からx=0.5で
x=0.5がNeumann境界のS=0です。
ですので未知数のu(0.5)は上で紹介したDirichlet-Dirichletと同じ値になるはずです。
下表にプログラムと計算結果を示します。
計算結果のu(0.5)と厳密解の絶対差を下のグラフに示します。
横軸は自由度のnです。
u(0.5)はDirichlet境界から一番遠くNeumann境界の点ですから誤差が最大になると考えられる。
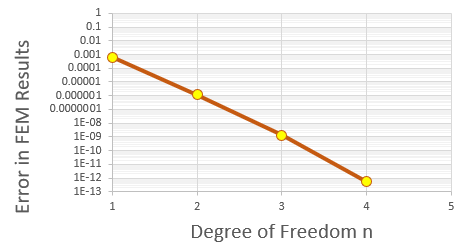 上の図を見るとn=4で誤差が倍精度の限界の1E-13のレベルまで達しています。
ほぼDirichlet-Dirichletと同じ精度に達しています。
倍精度計算を使っているので自由度nを増やしてもは計算精度の向上は期待できないと思われます。
試しに自由度n=5のプログラムを作成し計算を実施してみたが計算精度は自由度n=4とほぼ同じでした。
上の図を見るとn=4で誤差が倍精度の限界の1E-13のレベルまで達しています。
ほぼDirichlet-Dirichletと同じ精度に達しています。
倍精度計算を使っているので自由度nを増やしてもは計算精度の向上は期待できないと思われます。
試しに自由度n=5のプログラムを作成し計算を実施してみたが計算精度は自由度n=4とほぼ同じでした。
2つの例題を紹介しました。自由度を上げると計算精度は厳密解に近づくことが分かりました。
よってここで紹介した重み付け残差法はn=∞で厳密解を再現してくれると考えられます。
BACK
Linear Element
Menu
View
Helm
wrm
Lin
Element
Rmrk
Vari
Para
Non-L
Wire
Internet College of Finite Element Method