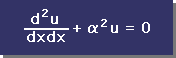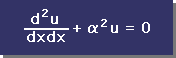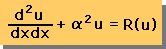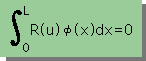One Dimensional Finite Element Method
Weighted Residual Method
■概 要■
有限要素法の話に入る前に、厳密解と近似解の違いについて述べておきます。
微分方程式の厳密解をその微分方程式に代入すると何も残りません。
ところが、その微分方程式の近似解を微分方程式に代入したら、どうなるでしょう。
今度は、誤差らしきものが残ります。
この誤差らしきものが、厳密解と近似解との差を表す残差(Residual) です。
近似解が、厳密解に近い程、Residualは小さくなります。
有限要素法では、このResidualに注目し、Residualを最小にする方法が考え出されました。
それが、このサイトで紹介する重み付け残差法(Weighted Residual Method) です。
ここでは、WRMとも呼ぶことにします。
つまり、有限要素法では、Residualが最小になる近似解を提供してくれていることになります。
余談ですが、重み付け残差法の原型は、変分法のbreakthroughと言われているEuler-Lagrange Equation(1759) が導出された過程で出てきていると考えられます。
なぜかと言うとEuler-Lagrange Equationと微分方程式は密接な関係に有るからです。
重み付け残差法では、5つの手続きが有りこれらを実施することにより与えられた問題の近似解を得ることができます。
| Procedures | Implementation Details |
|---|
| 1 | 当該微分方程式を使って残差を定義する |
|---|
| 2 | 積分式を立てる |
|---|
| 3 | 近似式𝑢(𝑥) を作る |
|---|
| 4 | 重み関数𝜙(𝑥)を作る |
|---|
| 5 | 積分式の2階微分項に部分積分法を施す |
|---|
■Residual■
では、早速、Residual から説明します。まず、解析したい微分方程式を 、L(u)+....=0 の形にします。下に示すHelmholtz equation は、
既に L(u)=0 の形になっています。ここで、L(u) の u は厳密解を意味します。
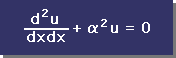 もし、式が L(u)=f(x) の場合は、L(u)-f(x)=0 とおきます。 そして、この u の代わりに、先ほど導いた近似式を代入します。
すると、 L(近似式)+....=0 にならず、=R(u) 残差が発生します。つまり、下の様になります。
下式の u は、近似解の u です。
もし、式が L(u)=f(x) の場合は、L(u)-f(x)=0 とおきます。 そして、この u の代わりに、先ほど導いた近似式を代入します。
すると、 L(近似式)+....=0 にならず、=R(u) 残差が発生します。つまり、下の様になります。
下式の u は、近似解の u です。
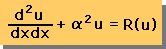 ■Integral Equation■
■Integral Equation■
Wieighted Residual Method では、R(u) を使って、下の左に示す積分式を計算することにより、近似解uを求めています。
ここに、u は近似解、φ(x)は重み関数(Weighting function)です。L は領域の長さを意味します。
また、下の左式のR(u)の代わりに、微分方程式を挿入すると、下の右図の様にも書けます。
この積分式は、与えられた重み関数と後ほど紹介する近似式で成し得る最良の近似解を提供してくれます。
つまり、残差またはuの誤差が最小になってることを保証してくれています。
上の積分式は、実は、変分法で言うFirst Variation(δI=0)の結果の式なのです。
変分法とは、与えられた問題を一旦最大最小の問題に置き換えてから、問題の未知数を解く手法です。
弾性解析では、平衡問題を仕事量の問題に置き換え、仕事量が最小になる変位または応力を求めています。
ところで、関数u(x)が最大か最小になっている点は、du/dx=0になっている点と教わりましたよね。
ではu(x)が引数になっている仕事量Iが有ったとします。その最小仕事量はどのようにして計算できるのでしょうか。
1つの方法として、いくつかのu(x)を準備し、それらで仕事量Iを計算し最小のIになっているのを正解としますよね。
この操作を自動でやってくれているのが変分法です。いくつかのu(x)のことを変分法では許容解と言います。
そして、上の積分式により直接その正解にたどり着くことができます。
上の積分式が最小値を与えてくれる式であることを発見したのがLagrangeです。彼が22歳のときでした。
この発見は、このとき50歳前後のEulerへ手紙で伝えられました。
現在では、上の積分式と等価で大最小の問題に置き換えた式がEuler-Lagrange Equation ととして知られています。
変分法の仕組みについては、後程、紹介する変分法(Calculus of Variations)で詳しく説明します。
また、文献 も参考にして下さい。
しかし、この段階でいきなり変分法から勉強に入るのはかなりの重荷になってしまいますので、
とりあえず、上の式を次の様に理解しておいて下さい:u が厳密解でない限り、R(u)の積分はゼロになりえない。
そこで、R(u)φ(x)を領域積分し、それを強制的にゼロとすることで、近似解を求める。
これにより、残差R(u)は、領域に分散され、領域内の解析精度も、一様化される。
この積分式ですが、微分方程式が線形の場合や、幾つかの非線形微分方程式に限り、近似式を無限級数で表せば、
厳密解に収束することが証明されています。
BACK
NEXT
Menu
View
Helm
wrm
Lin
Element
Rmrk
Vari
Para
Non-L
Wire
Internet College of Finite Element Method