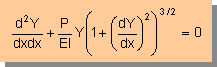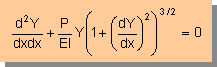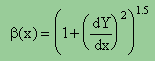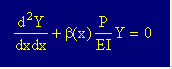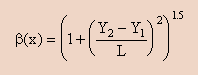One Dimensional Finite Element Method
Non-Linear Helmholtz Equation

■解析する非線形の式■
これまでは線形微分方程式を解いてきました。 線形だと最後に解く連立方程式も線形になりますね。 ところが線形でないと言うことになると微分方程式も連立方程式も非線形ということになります。 もし微分方程式の1つの項に u(x)2 が有るとします。 すると最後に解く連立方程式も2次になります(2次の連立方程式を解けないことはないが複雑な計算をしなければなりません)。 しかし u(x)1.5 の様な半端は乗数の項が微分方程式に含まれると話は違ってきます。 すんなりと数学的に解くことができまくなります。

この様に非線形微分方程式の解き方はケースバイケースになります。 つまり、これと言った万能な方法は有りません。 ここでは前に紹介した下の式の解き方を紹介します。 解き方としては最も簡単で理解し易い方法を紹介します。

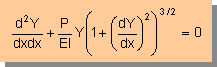
■Y(x)の Good Guess が必要■
突然ですが貴方なら非線形微分方程式をどの様に解きますか。 多分、非線形の部分を定数または xの関数とし 微分方程式を線形化しますよね。 つまり Y(x)を予測し解析の前に非線形の部分を計算してしまうということですね。 解析の後で予測のY(x)と計算されたY(x)を比較し予測が正しかったどうかを確認しますよね。

ここでも貴方の考えと同じ方法で話を進めることにします。 上の式を見ると dY(x)/dx は未知ですので計算できません。 そこで 計算の第1ステップとして線形微分方程式を解いたときと同じ仮定を使います。 つまり dY(x)/dx=0 です。 または Y(x)=constant です。 すると 計算の第2ステップとして解析結果から dY(x)/dx が計算できます。 ここでは非線形の部分を下式に示す様にβ(x)で置き換えることにします。

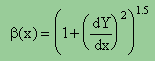ちょっと言い換えると 計算の第1ステップでは β(x)=1 だったと言うことですね。 ですから 計算の第2ステップのβ(x)は 更新された値と言うことになります。 そして その新しいβ(x)を使った線形微分方程式は 次の様になります。

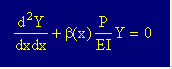上の式から計算されるY(x)を用いて再びβ(x)を計算し上の式を解きます。 これら一連の計算を繰り返すと Y(x) の値は だんだん落ち着いてきます。 結果的に計算は収束し解が得られたということになります。

■β(x)の積分と要素の関係■
この問題に限ってですが β(x)の値は 線形要素内(1次要素)において 下に示す様に一定値になりますね。 なぜかと言うと 線形近似のY(x)を微分すると一定値になるからです。

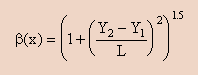しかし、2次要素を使うと β(x)は x の関数になり 積分が少々複雑になります。 そこで、ここでは、線形要素を使った例題を紹介します。
BACK to Parabolic Element NEXT
Menu View Helm wrm Lin Element Rmrk Vari Para Non-L Wire
Internet College of Finite Element Method