■Wire & Chain の概要■
非線形微分方程式の例題を、もう1つ紹介します。 それは、Wireのたわみです。 Wire の代表的なものとして、送電線がありますね。 送電線を短く切って観察すると、Elastic 材料ですよね。 つまり圧縮/引っ張り/曲げを支持できる。 しかし ある程度長くなると、Wire は、Chain と同じ様な性質を持つ様になります。 つまり (1)Tension のみで形を保っている。 (2)Elastic でない。 つまり 曲げ力を支持できない。 (3)Wireの傾きと力(Tension) のベクトルの向きが同じだと仮定できる。

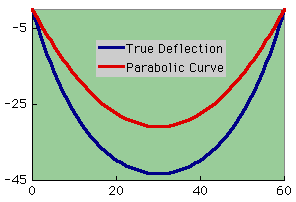
さて、本題にはいりましょう。 電柱間に張られた電線や 人の首にかけられたネックレスを見ると 2次曲線を描いている様に見えますよね。 ところが 実は非常に複雑な曲線を描いているのです。 しかし 電線の張力を大きくして行くと 2次曲線に近くなってきますがね。 下にChainのたわみが2次曲線(線形微分方程式)であると言う仮定のもとで解析した結果と、非線形微分方程式の計算結果を示します。 計算条件として、Chainの長さが112cm、質量が約40グラム、Chainを支持している2点間の距離が60cm、になっています。 詳細な解析結果は、後ほど紹介します。

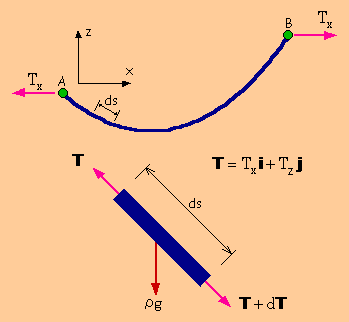
■ds長さのWire■
イントロは これぐらいにして 早速 Wireのたわみが計算できる微分方程式を導いてみましょう。 そのためには 下図に示す様にWireの一部分を切り取って力のバランス式を書く必要があります。 切り取ったWireの長さは ds とします。