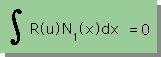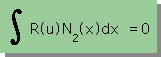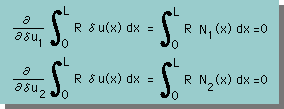Final Remark

One Dimensional Finite Element Method
Final Remark

■重み関数の新しい記述方法■
これまでの方法では積分式の書き表し方が面倒でした。つまり形状関数(重み関数)の数だけの積分式を書いていました。 2次元や3次元になると要素当たりの節点数が増えてきます。すると要素の節点の数だけの積分式を書かなくてはなりません。非常に面倒です。

ここでは重み関数の新しい記述方法を導入し積分式を1つにまとめる方法を学びます。新しい重み関数を紹介する前に、まず左下の1次要素の近似式を見てみましょう。当り前ですが要素内のu(x)を表すのに近似式は1つでOKです。

u(x) = u₁N₁ + u₂N₂

δu(x) = δu₁N₁ + δu₂N₂

重み関数も近似式の様に1行で書ける様にします。そのためにδu(x) と言う新しい変数を導入します。すると新しい重み関数は上の右式に示す様になります。ここにδu_iは、ゼロ以外の数値をもつ変数とします。詳細な説明は後程紹介します。すると積分式は次の様に書けます。

ここにLは要素の長さです。 (今までは主にLを領域の長さに、そしてL_iを要素の長さとしていましたが、ここではLは要素の長さとします。)
δu(x)は全ての節点の重み関数を含んでいるため I=0 と書くことが出来ません。このままでは、下の2つの積分式の計算が出来ません。ではどうすれば下の2つの積分式が計算出来るでしょうか。

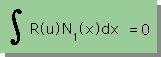と

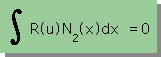ちょっと複雑になりますが以下の様にして求められます。つまり必要な積分式は何時でも導き出せることになります。

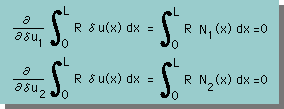
BACK-Element By Element Integration NEXT

Menu View Helm wrm Lin Element Rmrk Vari Para Non-L Wire Internet College of Finite Element Method