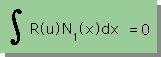 と
と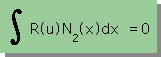
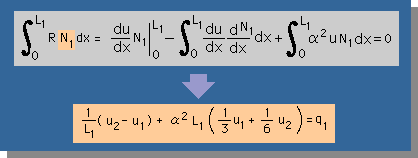
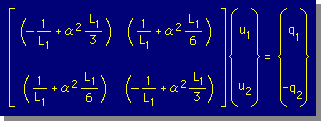
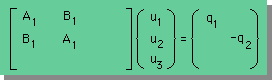
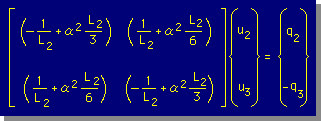
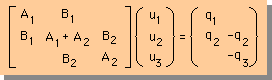
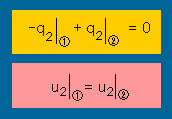
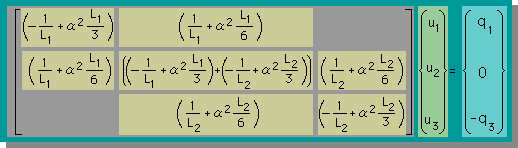
■Integral by Element のまとめ■
Linear Elementに引き続き
Integral by Elementで紹介した計算手順を紹介します。
この後1次元では新しい重み関数と2次要素が残っています。
ここで一服してもらうために Integral by Element で勉強した事柄をまとめてみましょう。
Integral by Element での計算手順(Linear Element の場合)
| 形状関数 N1(x)とN2(x)を準備する。 | N1(x)=1-x/L, N2(x)=x/L |
| 右に示す2つ積分式を立てる | 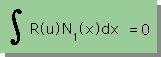 と と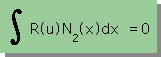
|
| 積分し、線形式を導く(R(u)N1の積分の場合) | 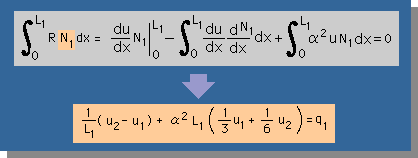 |
| 2つの積分式から、要素1の2X2の連立方程式を作る。 | 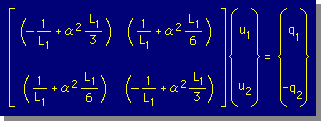 |
| Global連立方程式に上の連立方程式を足し込む。 | 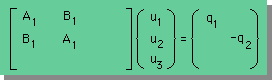 |
| 要素2についても同様な2X2の連立方程式を作る。 | 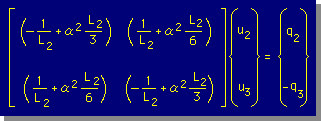 |
| Global連立方程式に上の連立方程式を足し込む。 | 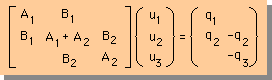 |
| Inter-Element Continuity を上の連立方程式の右辺に適用する。右の図の上側の条件 | 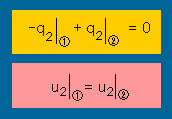 |
| Global連立方程式に上の連立方程式を足し込む | 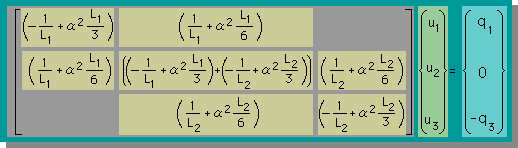 |
| Global連立方程式に境界条件を組み込み連立方程式を解く。 | |