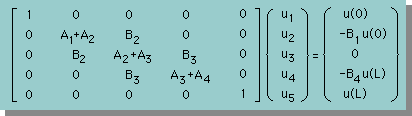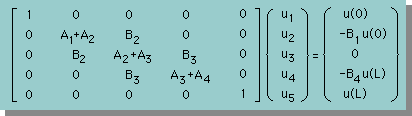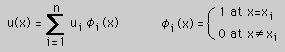One Dimensional Finite Element Method
Linear Element-11
■要素が4つの場合■
例えば領域を4要素で分割し要素の長さをそれぞれL1, L2, L3,L4, としてDirichilet境界条件を u1=u(0)と u5=u(L)とした場合の連立方程式は次の様になります。
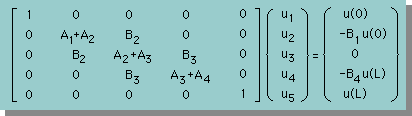
■部材が左右対称の場合■
左右対称ということは領域の中央でdu/dx=0になっているということです。境界条件と境界値は以下の表に示す通りでした。
| 位置 |
境界条件 |
境界値 |
| x=0 |
Dirichlet型 |
u1=u(0) |
| x=L/2 |
Neumann型 |
q=0 |
境界値のq=0 とはdu/dx=0 at x=L/2 を意味します。以下にL/2を2要素で分割したときの連立方程式を示します。

■1次要素の形状関数と近似式と重み関数のまとめ■
1次要素のまとめとして、ここでもう1度、形状関数と近似式と重み関数について復習しておきたいと思います。
- 形状関数
- 1次要素では2つの形状関数によって構成されています。形状関数は無次元です。
- 近似式
- 近似式は領域全体をカバーする関数です。
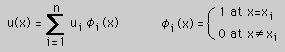
ここに関数
φi(x)は上式の右の条件を満足していなくてはならない。
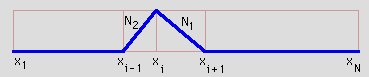
φi(x)を描画すると下図になる。
また下図に示す様に
φi(x) は形状関数のN2(x)とN1(x)で構成されていている。
- 重み関数
- 未知数 ui の重み関数φi(x)はxiでφi(xi)=1、他の点で
ゼロになっている。
そして関数は無次元になっている。
つまり、Galerkin method を使うと上の図のφi(x)が、未知数 ui の重み関数になります。
 問題
問題 疑問および質問
疑問および質問
BACK
NEXT
Menu
View
Helm
wrm
Lin
Element
Rmrk
Vari
Para
Non-L
Wire
Internet College of Finite Element Method