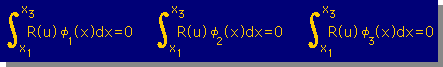
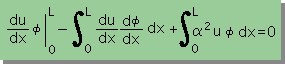
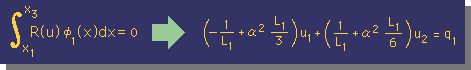
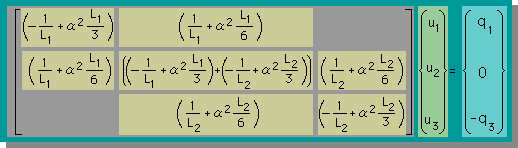
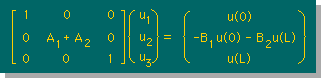
■Linear Elementのまとめ■
1次元有限要素法では最初に領域全体を表す近似式を使って近似解を得る方法をWRM(重み付け残差法)で紹介しました。 そして領域全体をLinear Elementで繋いだ近似式を紹介しました。近似式を図にすると折れ線グラフに見えましたね。 この後1次元では 要素毎の積分 、 新しい重み関数等が残っています。 ここで一服してもらうためにLinear Elementで勉強した事柄をまとめてみましょう。

Linear Element での計算手順

全領域を2つ以上の Linear Element で分割する
両境界と要素の繫ぎ目(節点と呼ぶ)に未知数(unknown)uiを付与する	u1, u2...............,un
形状関数 N1とN2を組み合わせて領域全体をカバーする関数 φiを作る	φ1, φ2...............,φn
近似式 u(x) をuiとφiから作る	u(x)=u1φ1 + u2φ2 +..........+ unφn
φiをuiの重み関数とする	φ1, φ2...............,φn
未知数(unknowns)の数だけの積分式を立てる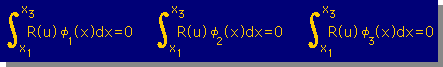
積分式の2階微分項に部分積分法を施す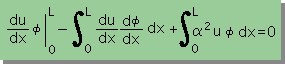
積分を行って線形式を導く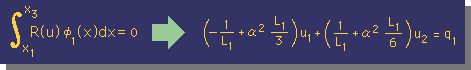
線形式を集めて連立方程式を作る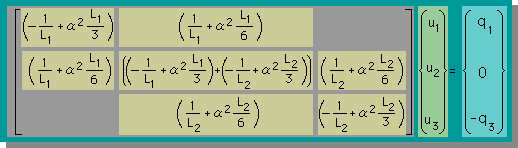
例: 両端にDirichlet型境界条件を連立方程式に組み込む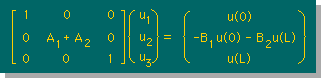
例: 左端がDirichlet型、右端がNeumann型境界条件(q=0)を連立方程式に組み込む
連立方程式を解く

ここではWRM(重み付け残差法)と同様に領域全体を積分する方法を学びました。 もー、貴方は気付いたと思いますが、要素毎に積分できそうですね。 と言うことで次では要素毎の積分を試みてみます。