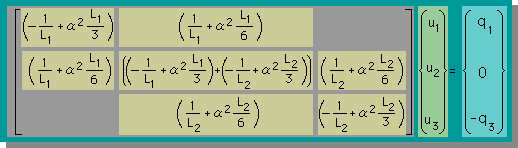
■u₂,q₁, q₃を一括計算 ■
linearelement-10の続きですが、 読者から”u₂,q₁, q₃を同時に計算できないのですか”と言う質問をうけました。 答えは”出来ます”です。 しかし機械的に計算する上で非効率な方法と言えます。 ですから有限要素法ではuとqは別々 に計算します。 参考までにu₂,q₁, q₃を一括で計算する方法を紹介しておきます。

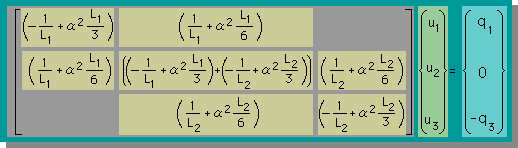
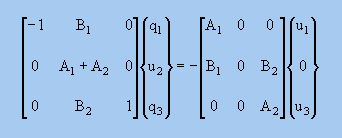
■WRMの近似式とLinear Elementの近似式の違い■
WRMで紹介した近似式には、 φ₀が有り境界条件のみを取り込めるようになっていました。 しかしLinear Elementで紹介した近似式にはφ₀は有りませんでした。 Dirichlet境界では未知数u₁またはu_nを使うことにより問題なく境界値を取り込むことができました。
ではNeumann境界ではどうでしょう。 WRMの近似式の場合φ₀にNeumann境界の境界値を取り込み、尚且つ積分式にも境界値が存在しました。 Linear Elementの近似式にはNeumann境界の境界値は取り込めません。積分式のみに境界値が入ります。 ではLinear ElementでNeumann境界が与えられた問題を解いた場合、近似解はNeumann境界で境界値になっているのでしょうか。 答えは領域の分割数を増やすと境界値に近づくです。 領域の右端がNeumann型境界とした場合を例に取り上げます。 3つ目の積分式を見て下さい。 この代数式のL₂=Δx, u₃-u₂=Δuとすると以下の式になります。 \begin{eqnarray} \frac{\Delta u}{\Delta x}=q_3+\alpha^2\Delta x \left(\frac{u_2}{6}+\frac{u_3}{3}\right) \end{eqnarray} Δx→0のリミットをとると以下の結果になります。 \begin{eqnarray} \frac{du}{dx}=q_3 \end{eqnarray} つまり、領域の分割数を増やす(Δx→0)とLinear Elementの近似式はNeumann型境界の境界値に近づくことになります。