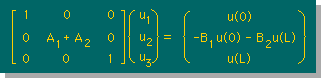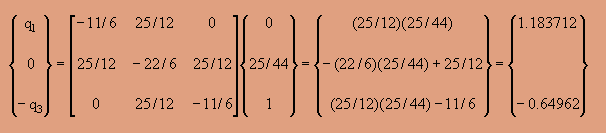One Dimensional Finite Element Method
Linear Element-10
■Dirichlet境界条件を組み込む■
それではこの連立方程式にDirichlet境界条件を組み込んでみましょう。
境界条件は下の示す通りとします。
| 境界条件 | 境界値 | つまり |
|---|
| u(x) at x=0 | u(0) | u1=u(0) |
| u(x) at x=L | u(L) | u3=u(L) |
連立方程式には未知数が3つ有ります。
その内の2つがDirichlet境界条件として与えられているので計算で求まる未知数は1つ(u2)になります。
つまり連立方程式の2行目があれば問題は解決することになります。
しかしこの方法は機械的に解析するという点からみると賢い方法とは言えません。
機械的に且つ効率的に解析出来るようにするには次のルールを守る必要があります。
| マトリックス[K]の大きさを維持する。 |
| [K]が対称マトリックスであればDirichlet境界条件組み込んだ後も[K]を対称に保つ。 |
上の2つをルール化すると次の様になる。
| Dirichlet境界条件を連立方程式に組み込むルール |
| 1 |
Dirichlet境界条件が組み込まれる行(row)に存在している全ての値をゼロにする。
そして、その行のマトリックスの対角要素の位置に1を挿入し、右辺のその行の位置に境界値を挿入する。 |
| 2 |
マトリックスと未知数ベクトルの掛け算を行いDirichlet境界条件と掛け算される項は全て右辺へ移動する。 |
ちょっと理解しにくそうですので実際にやってみましょう。
その前にグラフィックのスペースを節約するためにマトリックスの中にある数値を次の様に置き換えます。
すると領域の両端にDirichlet境界条件を組み込んだ連立方程式は次の様になります。
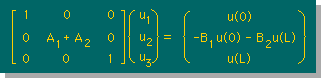この結果を用いてu(0)=0, u(L)=1, L1=L2=0.5, α2=1 で計算してみると
u2=25/44=0.56818
が得られます。
貴方も確認してみて下さい。
そして計算されたu2と境界条件として使ったu1とu3を
境界条件を挿入する前の式に投入すると
q1とq3を得ることが出来ます。
実際に数値を代入すると、以下のようになります。
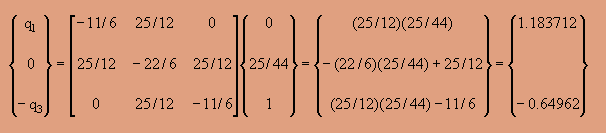
結果的に、q1=1.183712, q3=0.64962になります。
BACK
NEXT
Menu
View
Helm
wrm
Lin
Element
Rmrk
Vari
Para
Non-L
Wire
Internet College of Finite Element Method