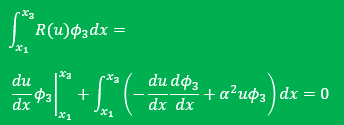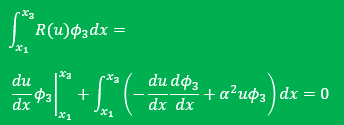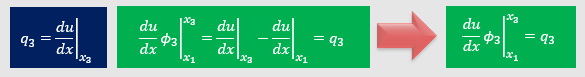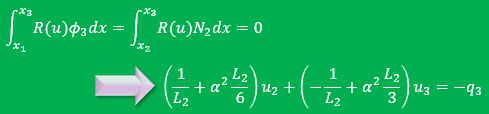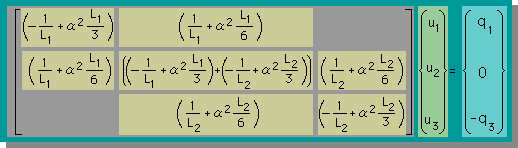One Dimensional Finite Element Method
Linear Element-9
■3つ目の積分式■
最後に3番目の積分式ですがこれは最初の積分式のとよく似ています。
未知数と定数を入れ替えるだけで積分結果は得られます。但し境界積分に注意して下さい。
まず積分式と重み関数を下に表示しておきます。
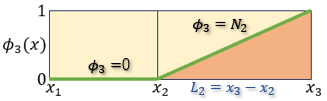
領域x1からx2まではφ3=0ですから積分範囲に加える必要はありません。
領域x2からx3まではφ3=N2になっています。
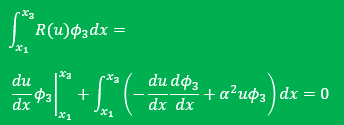
 φ3(x1)=0だから積分式の境界積分項は以下のようになります。
またx3でのdu/dxをq3と定義します。
これはNeumann境界条件の境界値になります。
φ3(x1)=0だから積分式の境界積分項は以下のようになります。
またx3でのdu/dxをq3と定義します。
これはNeumann境界条件の境界値になります。
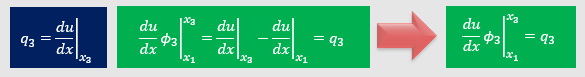 積分はこれまでに紹介して1つ目の積分式と2つ目の積分式から拾い集めることができます。
結果は次の様になります。
積分はこれまでに紹介して1つ目の積分式と2つ目の積分式から拾い集めることができます。
結果は次の様になります。
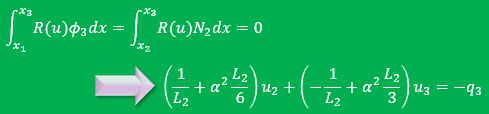 以上全ての積分式が計算出来たところで結果を1つの連立方程式にまとめてみましょう。
下がそうです。
以上全ての積分式が計算出来たところで結果を1つの連立方程式にまとめてみましょう。
下がそうです。
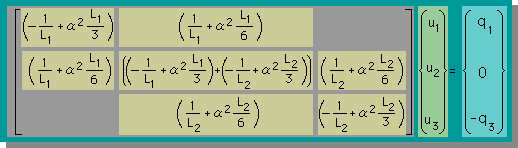 この連立方程式を有限要素法では[K]{u}={q}と書きこの[K]を”通称”剛性マトリックスといいます。
ここで貴方に1つだけ注意しておきますが上の連立方程式にDirichlet境界条件はまだ組み込まれていません。
WRMで紹介した近似式の
φ0(x)に
Dirichlet境界条件またはNeumann境界条件が既に組み込まれていました。
ここではu1とu3に値を与えることによりDirichlet境界条件が組み込まれます。
この連立方程式を有限要素法では[K]{u}={q}と書きこの[K]を”通称”剛性マトリックスといいます。
ここで貴方に1つだけ注意しておきますが上の連立方程式にDirichlet境界条件はまだ組み込まれていません。
WRMで紹介した近似式の
φ0(x)に
Dirichlet境界条件またはNeumann境界条件が既に組み込まれていました。
ここではu1とu3に値を与えることによりDirichlet境界条件が組み込まれます。
BACK
NEXT
Menu
View
Helm
wrm
Lin
Element
Rmrk
Vari
Para
Non-L
Wire
Internet College of Finite Element Method