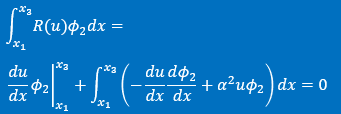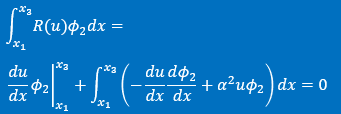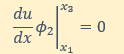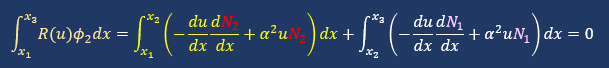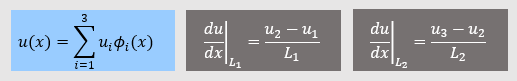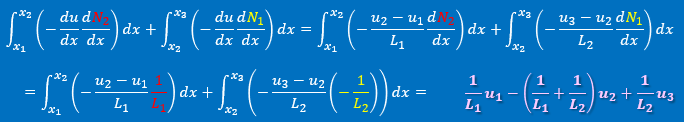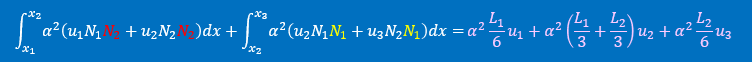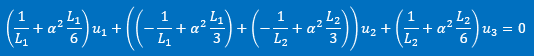One Dimensional Finite Element Method
Linear Element-8
■2つ目の積分式■
まずその積分式と重み関数を下に示します。
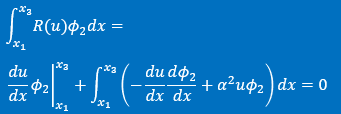
 境界積分項ですが
φ2(x1)と
φ2(x3)はゼロですから以下の結果になります。
よって積分式から境界積分項を削除出来ますね。
境界積分項ですが
φ2(x1)と
φ2(x3)はゼロですから以下の結果になります。
よって積分式から境界積分項を削除出来ますね。
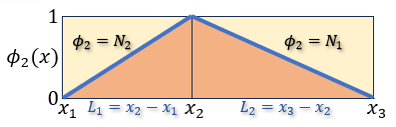
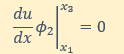 上図の重み関数φ2ですが座標x1からx2まではN2で
座標x2からx3まではN1で構成されています。これらを積分式に取り込むと以下になります。
上図の重み関数φ2ですが座標x1からx2まではN2で
座標x2からx3まではN1で構成されています。これらを積分式に取り込むと以下になります。
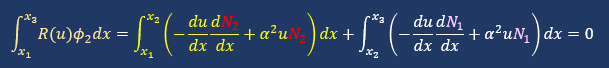 下の近似式u(x)は座標x2からx3までは
u(x)=u2N1+u3N2と書けることを頭に入れておいてください。
そして領域L1とL2におけるu(x)の微分は以下になります。
下の近似式u(x)は座標x2からx3までは
u(x)=u2N1+u3N2と書けることを頭に入れておいてください。
そして領域L1とL2におけるu(x)の微分は以下になります。
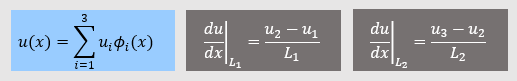 まず上の積分式の微分項を計算してみました。以下の代数式ができます。
まず上の積分式の微分項を計算してみました。以下の代数式ができます。
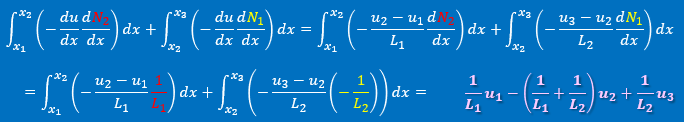 領域L1にある積分式のα2の項のuN2は
uN2=u1N1N2+u2N2N2
と書けますので、この項の積分は最初の積分式を参考にして下さい。
α2の項の積分は以下のようになります。
領域L1にある積分式のα2の項のuN2は
uN2=u1N1N2+u2N2N2
と書けますので、この項の積分は最初の積分式を参考にして下さい。
α2の項の積分は以下のようになります。
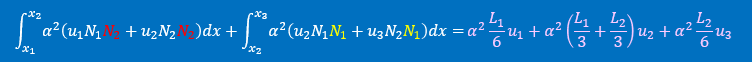 上の2式を足すと2つ目の積分式の結果として最終的に以下が得られます。
上の2式を足すと2つ目の積分式の結果として最終的に以下が得られます。
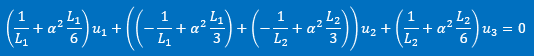
BACK
NEXT
Menu
View
Helm
wrm
Lin
Element
Rmrk
Vari
Para
Non-L
Wire
Internet College of Finite Element Method