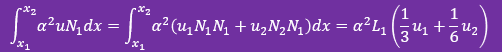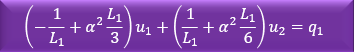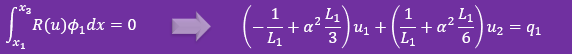One Dimensional Finite Element Method
Linear Element-7
独立変数がないということは積分を行うときに座標軸の変数を自由に行えるということです。
ちょっと解りにくいので下図で説明します。
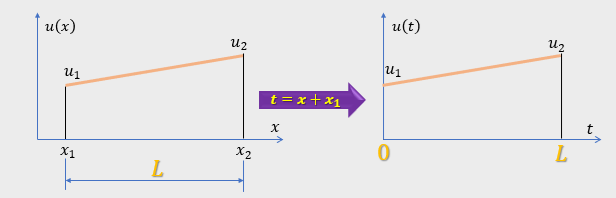 左図の座標軸はxです。そして、右はtです。
両者を関係付けているのが、t=x-x1です。この様に座標変換を行うと積分が随分楽になります。
この方法で形状関数N2(x)の二乗とN1(x)×N2(x)の積分結果を下に示しますので
貴方も計算してみて下さい。同様な手順でN1(x)の二乗の積分を行うと∫N1N1dt=L/3になります。
左図の座標軸はxです。そして、右はtです。
両者を関係付けているのが、t=x-x1です。この様に座標変換を行うと積分が随分楽になります。
この方法で形状関数N2(x)の二乗とN1(x)×N2(x)の積分結果を下に示しますので
貴方も計算してみて下さい。同様な手順でN1(x)の二乗の積分を行うと∫N1N1dt=L/3になります。
 するとu(x)N1(x)の積分は次の様になります。
するとu(x)N1(x)の積分は次の様になります。
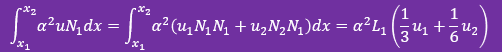 よって積分式の結果は下に示す様に未知数と変数(αとL)と定数から成る線形代数式になります。
よって積分式の結果は下に示す様に未知数と変数(αとL)と定数から成る線形代数式になります。
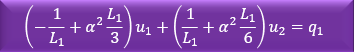 結果的に最初の積分式から以下の代数式が得られたことになる。この代数式は全て3つの積分式が得られたら
連立方程式に組み込むことになります。
結果的に最初の積分式から以下の代数式が得られたことになる。この代数式は全て3つの積分式が得られたら
連立方程式に組み込むことになります。
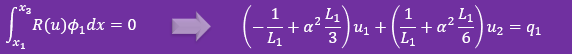 この時点で、貴方にチェックしてもらいたい作業があります。
それは右辺と左辺の次元のチェックです。
この作業は大切ですので必ず行って下さい。
右辺と左辺の次元が異なっている場合は積分を行っている最中に間違った作業を行っているはずです。
尚、du/dx=q1が無次元でα2は[1/L2]です。
この時点で、貴方にチェックしてもらいたい作業があります。
それは右辺と左辺の次元のチェックです。
この作業は大切ですので必ず行って下さい。
右辺と左辺の次元が異なっている場合は積分を行っている最中に間違った作業を行っているはずです。
尚、du/dx=q1が無次元でα2は[1/L2]です。
BACK
NEXT
Menu
View
Helm
wrm
Lin
Element
Rmrk
Vari
Para
Non-L
Wire
Internet College of Finite Element Method