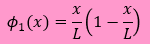One Dimensional Finite Element Method
Linear Element
■今までの近似式■
ここで、もう一度、今まで使っていた近似式を観察してみましょう。
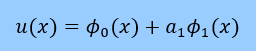 ここに
ここに
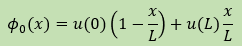 、
、
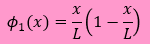 近似式をちょっと並び替え1次要素の形状関数を使うと次の様に書けます。
近似式をちょっと並び替え1次要素の形状関数を使うと次の様に書けます。
|
\begin{eqnarray}
u(x)=u(0)N_1(x)+u(L)N_2(x)+a_1N_1(x)N_2(x)
\end{eqnarray}
|
ここに
|
\begin{eqnarray} N_1(x)=\left(1-\frac{x}{L}\right) \end{eqnarray}
|
\begin{eqnarray} N_2(x)=\left(\frac{x}{L}\right) \end{eqnarray}
|
です。
u(x)は変数×関数の集りで表わされています。
ここに、変数とはu(0)、a1、u(L)のことでu(x)と同じ単位をもっています。
関数は無次元であり変数が関係する点または領域では値があり
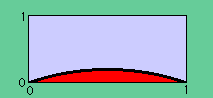
他の点ではゼロになっていますね。下の図を見て下さい。
 |
 |
 |
| \begin{eqnarray} N_1(x)=\left(1-\frac{x}{L}\right) \end{eqnarray} |
\begin{eqnarray} N_2(x)=\left(\frac{x}{L}\right) \end{eqnarray} |
\begin{eqnarray} N_1(x)N_2(x)=\left(1-\frac{x}{L}\right) \left(\frac{x}{L}\right)\end{eqnarray} |
例として、関数
N1
はu(0)が指定されている点(x=0)で値1をもち、x=Lの点ではゼロになっています。
関数
N2
も同様なことが言えます。
関数
N1N2
ではx=L/2で1/4の値をもち、x=0とx=Lでゼロになる2次曲線です。
変数a1には微分方程式のα2が反映されていています。
またa1はu(x)と同じ単位をもっています。
有限要素法で用いられる近似式ではa1の様な中途半端な変数は用いず座標xで指定された点での未知数u(x)の値を持つ変数を使います。
下式がそうです。
また、この式には、これまでの近似式
u(x)=
φ0(x)+a1
φ1(x)
の中で境界条件のみを満足している関数φ0(x)も下式に融合されることになります。
新しい近似式も参考にして下さい。
|
u(x)=
u1φ1(x)+
u2φ2(x)+
u3φ3(x)+
...........................+
un+φn(x)
|
つまり、近似式として下図に示す関数を使ってWRMで微分方程式を解くと求まる未知数uiは、全て指定された座標点xiでのu(x)になります。
下図は、全領域を1つの2次要素で表した例です。
(1次要素の場合は、既にWRMで概略を紹介してあります。)
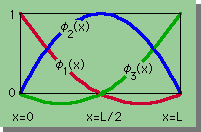 そして、その近似式は次の様に書けます。
そして、その近似式は次の様に書けます。
|
\begin{eqnarray}
u(x)=
u(0)\phi_1(x)+
u(L/2)\phi_2(x)+
u(L)\phi_3(x)
\end{eqnarray}
|
このように、2次式で書かれた近似式をもつ要素を2次要素と言います。
2次要素は、後で取り上げるとして、ここでは、まず1次要素(Linear Element)を紹介します。
BACK to WRM
NEXT
Menu
View
Helm
wrm
Lin
Element
Rmrk
Vari
Para
Non-L
Wire
Internet College of Finite Element Method
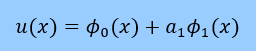 ここに
ここに
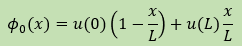 、
、
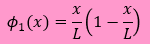
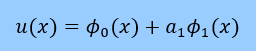 ここに
ここに
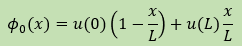 、
、