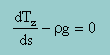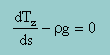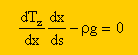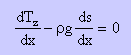One Dimensional Finite Element Method
Wire and Chain-2
前ページの図のTは、wire(ds)の左端に発生しているTension(張力)です。
Wireに作用している唯一の外力は、ρg と仮定しています。
すると、距離 ds 行った点(dsの右端)でのTensionは、T+dT になっているはずです。
実際は、dTに負の値が入っていますげね。
なぜかと言うと、wire の端の方が、中央付近よりTensionは大きい値になっていますからね。
話の材料が揃ったところで、ΣF=0をとってみましょう。
まず、ΣFx=0 を見てみます。下式がそうです。
上式から言えることは dTx=0 ですから
と言うことになりますね。
どういうことかと言うと、wire のどの部分(ds)を切り取っても その wire を支える Tension の x成分(水平方向)は一定と言うことです。
”当たり前なことじゃないか”とお思いでしょうが、この発見が後で大変役立つのですよ。
次に ΣFz=0 を見てみましょう。
下式がそうです。
すると z 方向には 下の微分方程式が得られます。
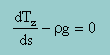 そしてChain rule を左辺の第1項に施すと次の様になります。
そしてChain rule を左辺の第1項に施すと次の様になります。
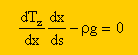 さらに上式の両辺に ds/dx をかけると下の様になりますね。
さらに上式の両辺に ds/dx をかけると下の様になりますね。
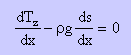 ところで dTz/dx から どの様にすれば Wire の座標を計算できる微分方程式にすることができるのでしょうか。
答えのヒントは 次のページ図をにあります。
ところで dTz/dx から どの様にすれば Wire の座標を計算できる微分方程式にすることができるのでしょうか。
答えのヒントは 次のページ図をにあります。
BACK
NEXT
Menu
View
Helm
wrm
Lin
Element
Rmrk
Vari
Para
Non-L
Wire
Internet College of Finite Element Method