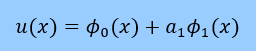 ここに
ここに
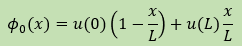 、
、
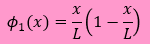
| 重み関数の条件 |
|---|
| 重み関数は、連続であること。 |
| Dirichlet境界において重み関数は、値がゼロである。 |
| Neumann境界において重み関数は、値が1で微分値がゼロである。 |
| 重み関数は無次元である。 |
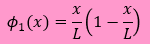 です。
φ1(x)は両境界でゼロになっています。
です。
φ1(x)は両境界でゼロになっています。
このように、近似式の一部を重み関数として使う方法を Galerkin's Method といいます。
ここで取り上げる最初の問題は、 u(0)とu(L)が既知のDirichlet境界条件なので、両境界点での重み関数値は、ゼロです。 つまり、境界での重み関数値は、a1の計算には、必要ないということです。 注意:Neumann型境界の取り扱いについては、次のSectionで詳しくお伝えします。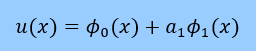 ここに
ここに
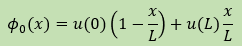 、
、
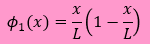
 |
 |
 |