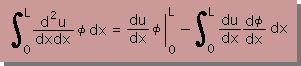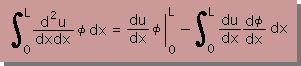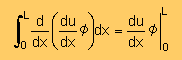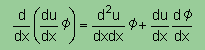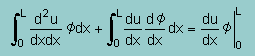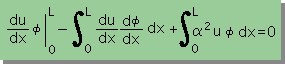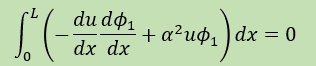Weighted Residual Method

One Dimensional Finite Element Method
Weighted Residual Method-3

■Integration By Parts■
重み関数が見つかれば次は、部分積分法を用いて、積分式の中の2階微分項の処理です。この処理を行うことにより、2階微分項は、1階微分の積分と境界積分に分離されます。したがって、部分積分法を積分式に施すことにより、下表の様な、有限要素法固有の特徴が現れてきます。

特　徴	解　説
近似式に線形の式が使える。	2階微分項があると近似式は最低xの2次式でなくてはならない。
境界条件を直接与えることが出来る。	Neumann Type 境界が式中に現れてくるので、境界値を直接与えることが出来る。

では早速、2階微分項を、部分積分で展開してみましょう。下式の様になります。

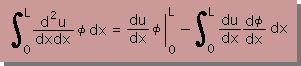”ちょっと分かりません”という方に、部分積分を、もう少し噛み砕いて説明しましょう。まず、下の式を見て下さい。これは、単なる定積分の定義ですよね。

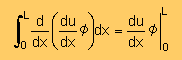ところで、上式の左辺ですが、積分される内容は、下式に示す様に、2つの項目に展開できますよね。 2つの関数の積の微分方法ですね。分からない人は、昔習った数学の本を開いて下さい。

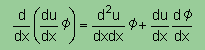と言うことは、上式の結果をその上の積分式に代入すると、次の様になります。そして、左辺の第2項を右辺へ移動すると、最初に紹介した部分積分の式になりますね。

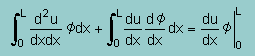部分積分は、有限要素法で頻繁に出てきますので、今うちにマスターしておいて下さい。

■Finite Element Equation■
さらに上式と∫R(u)φdx=0より下式が得られます。この式のことを通常 Helmholtz Equation の有限要素式( Finite Element Equation )と呼ばれます。

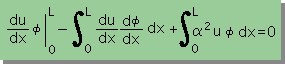ここまで来れば、Helmholtz Equationに対する有限要素法の仕事は50%終えたと思って良いでしょう。この後は、いかにして有限要素式を数値的に解くかです。
話を前に進めましょう。 Dirichlet境界条件を領域の両端に与えた時の重み関数 φ(x)=φ₁(x) は、x=0 と x=L でゼロですから境界積分の項は消えてなくなります。従って有限要素式は次の様になりますね。

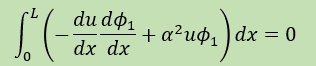
BACK NEXT

Menu View Helm wrm Lin Element Rmrk Vari Para Non-L Wire Internet College of Finite Element Method