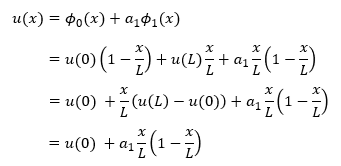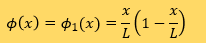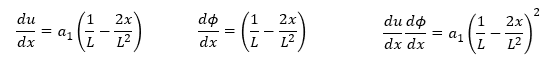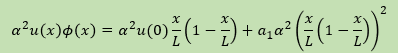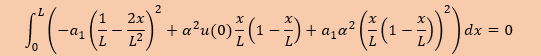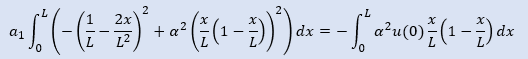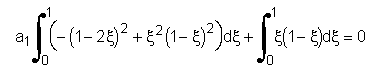One Dimensional Finite Element Method
Weighted Residual Method-4
■例題1:両境界がDirichlet境界■
練習のために、問題を解いてみよう。
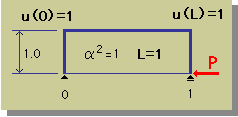
領域の長さはL=1で、α2=1で、u(0)=u(L)=1 とします。領域の長さはL=1とします。
丁度、下図に示す様な状況ですね。
 近似式は u(0)=u(L)の条件から次のようになりますね。
近似式は u(0)=u(L)の条件から次のようになりますね。
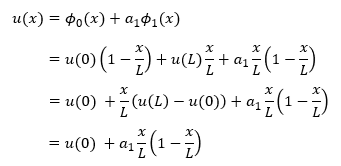 重み関数は Galerkin's Method より以下の様になります。
重み関数は Galerkin's Method より以下の様になります。
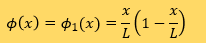 近似式と重み関数の微分とそれらの積は次のようになりますね。
近似式と重み関数の微分とそれらの積は次のようになりますね。
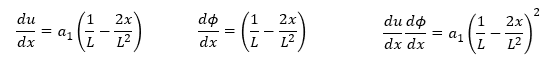 α2と近似式と重み関数の積は以下の様になります。
α2と近似式と重み関数の積は以下の様になります。
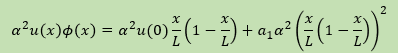 上の2つを積分式に代入すると以下のような簡単な積分になります。
上の2つを積分式に代入すると以下のような簡単な積分になります。
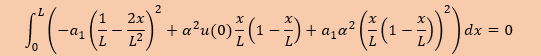 下は上をちょっと並び替えてあります。a1に関する項目を左辺に、その他は右辺に移動しました。
そしてa1について解けば近似解が得られます。
下は上をちょっと並び替えてあります。a1に関する項目を左辺に、その他は右辺に移動しました。
そしてa1について解けば近似解が得られます。
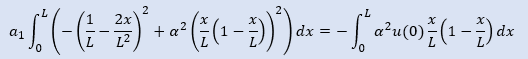 計算を簡単にするために座標変換を行います。x/L=ξと置きます。すると、dx=Ldξになります。
L=1でしたからdx=dξになりますね。
α2=1でしたから、上の積分は下のように成ります。
貴方も、やってみてくださいね。
計算を簡単にするために座標変換を行います。x/L=ξと置きます。すると、dx=Ldξになります。
L=1でしたからdx=dξになりますね。
α2=1でしたから、上の積分は下のように成ります。
貴方も、やってみてくださいね。
上の積分式を分解すると、次の3つの積分項に分けられます。
積分式の中の未知数は、a1 のみです。上の結果を積分式に代入すると、下の代数式が残ります。
そして、a1 について計算すると、a1=5/9になります。
この数値を近似式
に代入し、x=1/2 の点で u(x) を計算するとu(1/2)=1.1388888になります。
厳密解と比較すると誤差は0.0006になります。
先へ進む前に、是非、この問題をやって下さい。
今後、この問題を中心に、話しを進めて行きますので。
今まで学習した事をまとめてみましょう。近似式の中に含まれる未知数(Unknown)の数は1つでした。
計算に使った積分式も1つでした。更に、重み関数の数も1つでした。
つまり、有限要素法で微分方程式を解く場合、次のことがらが言えます。
| 近似式の中に含まれる未知数(Unknown)の数だけの積分式と重み関数が揃ったときに、未知数(Unknown)は、
uniquely に求めることが出来る。 |
BACK
NEXT
Menu
View
Helm
wrm
Lin
Element
Rmrk
Vari
Para
Non-L
Wire
Internet College of Finite Element Method