One Dimensional Finite Element Method
Weighted Residual Method-5
■自由度が1で両境界がDirichlet境界条件の場合のまとめ■
先へ進む前に、もう一度、練習で使った近似式を観察してみましょう。
近似式は、次の様に書かれていました。
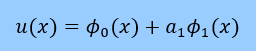 ここに
ここに
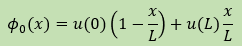 、
、
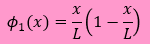 近似式を作るにあたって両境界がDirichletの場合の必要な事柄を下表にまとめておきます。
近似式を作るにあたって両境界がDirichletの場合の必要な事柄を下表にまとめておきます。
|
φ0にはDirichlet境界条件の境界値のみが盛り込まれている。よって、
φ0(0)=u(0), φ0(L)=u(L)
|
|
φ1はα2の変化のみに対応しDirichlet境界条件の境界値に影響を与えない。
よって、φ1(0)=0, φ1(L)=0
|
重み関数はGalerkin's Methodによりφ(x)=φ1(x)とした。
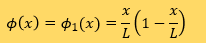
積分式はφ1(0)=0および
φ1(L)=0
より境界積分の項はゼロになる。よって積分式は以下になる。
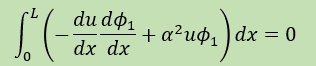
a1を機械的に計算
これまでは、少々強引に計算をすすめてきましたが、ここからは未知数であるa1を機械的に計算する方法を学びます。
機械的に計算するということは計算プロセスをプログラミングに取り込むことができます。
積分式に近似式を代入すると次の様に書けます。
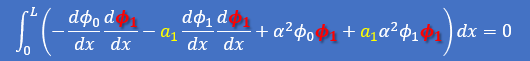 そしてちょっと並び替えると次の様になります。
そしてちょっと並び替えると次の様になります。
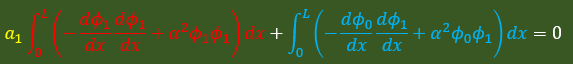 2つの積分はφの添え字を無視すれば、積分式とまったく同じですね。
丁度、積分が2つに分離されている状態になっています。理由は Helmholtz Equation が線形であるからです。
これは下の式からも説明ができます。
2つの積分はφの添え字を無視すれば、積分式とまったく同じですね。
丁度、積分が2つに分離されている状態になっています。理由は Helmholtz Equation が線形であるからです。
これは下の式からも説明ができます。
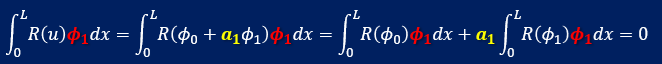
更に、上の積分を下に示す関数 H(f,g)で表すことにします。
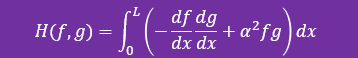 すると積分式は下に示すようにシンプルな形になります。
すると積分式は下に示すようにシンプルな形になります。
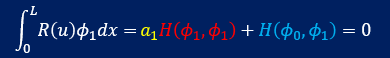 この関数 H(f, g) は、H(f, g) = H(g, f)であることを理解しておいて下さい。
この方法を用いると未知数a1は、以下でで計算できます。
プログラムでは、この関数をサブプログラム化にしておくことで問題を機械的に解くことができます。
この関数 H(f, g) は、H(f, g) = H(g, f)であることを理解しておいて下さい。
この方法を用いると未知数a1は、以下でで計算できます。
プログラムでは、この関数をサブプログラム化にしておくことで問題を機械的に解くことができます。
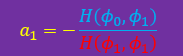 上の式が計算できるということは
H(φ1, φ1)
がゼロでないという条件が発生します。
上の式が計算できるということは
H(φ1, φ1)
がゼロでないという条件が発生します。
 問題
問題
BACK
NEXT
Menu
View
Helm
wrm
Lin
Element
Rmrk
Vari
Para
Non-L
Wire
Internet College of Finite Element Method
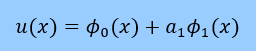 ここに
ここに
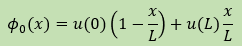 、
、
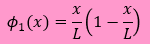
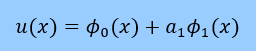 ここに
ここに
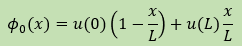 、
、
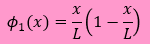
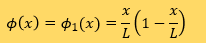
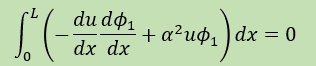
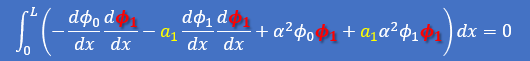
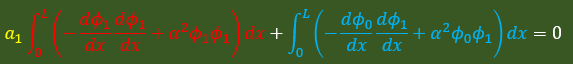
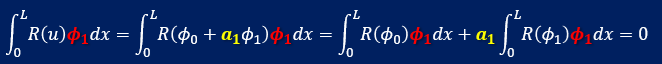
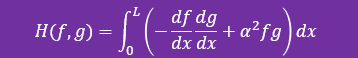
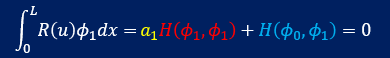
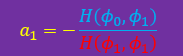
 問題
問題