One Dimensional Finite Element Method
Weighted Residual Method-6
■両境界がDirichletで自由度が2の近似式■
さて、自由度が2の場合の Helmholtz Equation の有限要素法はどうなるのでしょうか。
つまり、近似式に2つの未知数(Unknowns) が有る場合のことです。1つの考えとして下式があります。
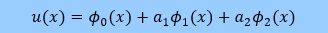 ここに
ここに
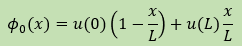 、
、
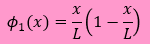 、
、
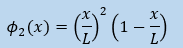 φ2(x)ですが両境界での条件は、φ1(x)と同じです。
つまり、φ2(0)=0とφ2(L)=0です。
φ2(x)ですが両境界での条件は、φ1(x)と同じです。
つまり、φ2(0)=0とφ2(L)=0です。
この様に、未知数が2つの場合は、先ほどの議論より、2つの積分式と2つの重み関数が必要になってきます。
運良く、2つ目の重み関数として条件をクリアーしているφ2(x)が使えそうです。
すると、2つの積分式は次の様になります。
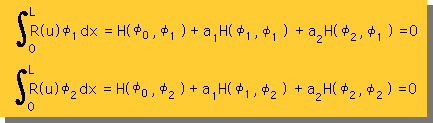 これをマトリックスの形で書くと次の様になり、未知数 a1とa2について計算することが出来ます。
これをマトリックスの形で書くと次の様になり、未知数 a1とa2について計算することが出来ます。
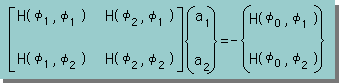 2つ目およびそれ以降の重み関数の条件
2つ目およびそれ以降の重み関数の条件
上で2つの重み関数が必要と言いましたが、勝手に適当に2つの重み関数を作っても良いのでしょうか。
2つ目の重み関数を決めるための条件はないのでしょうか。
答えは、2つ目以降の重み関数には、厳しい条件が要求されます。
その条件とは以下です。
|
上の2×2 のマトリックスの行列値(Determinant)はゼロであってはならない
|
|---|
この条件をクリアーしないと未知数(a1とa2)は計算されないですよね。
例えば、φ2(x)=cφ1(x) はどうでしょう。
先ほどの2×2 のマトリックスの行列値はどのような値になるでしょうか。答えはゼロです。
従って、φ2(x)は、φ1(x)に対し独立関数でなくてはなりません。
つまり、次の条件を守らなくてはなりません。
| 重み関数の条件(追加) |
|---|
| 各々の重み関数は、互いに独立関数でなくてはならない。 |
同様に近似式に使われる関数も互いに独立関数でなくてはならないのです。
関数 f(x)とg(x)とh(x)がある場合、関数f(x)は
| f(x)=定数×g(x) でないこと |
f(x)=定数×g(x) + 定数×h(x)でないこと |
 問題
問題
BACK
NEXT
Menu
View
Helm
wrm
Lin
Element
Rmrk
Vari
Para
Non-L
Wire
Internet College of Finite Element Method
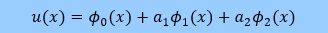
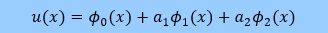
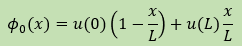 、
、
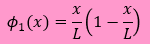 、
、
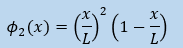
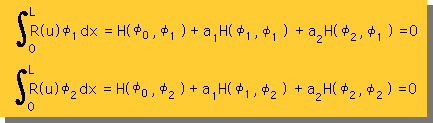
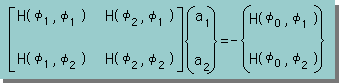
 問題
問題