One Dimensional Finite Element Method
Helmholtz Equation: A Buckling Problem-7

■Helmholtz Equation のまとめ■

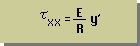
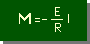
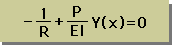
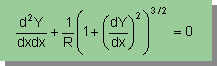
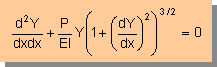
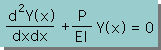
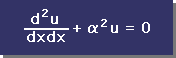
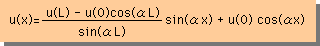
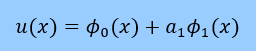
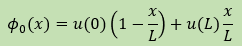
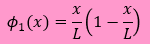
両端にモーメントがかかっているBeam

外力(P)による、点xでの曲げモーメントは、右の式で与えられる。 Mp=Y(x)P
Beam内のτxxは右の式で与えられる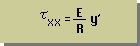
点xでのBeam内に発生している曲げモーメントは右の式になる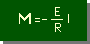
ΣMz=0 より右の結果が得られる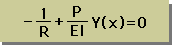
円の式
円の微分方程式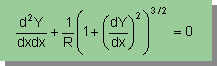
ΣMz=0 の結果を円の微分方程式に代入すると右式になる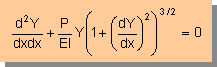
(dx/dx)2=0 と仮定すると右のHelmholtz Equation になる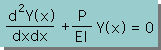
Helmholtz Equation の未知数にu(x)を用いる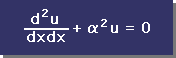
Dirichlet型境界条件 u(x)が境界で指定する
Neumann型境界条件 du/dx が境界で指定する
両端がDirichlet型境界の場合のHelmholtz Equation の厳密解は右の様になる。αL=nπは固有値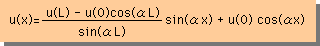
両端がDirichlet型境界の場合の最もシンプルなHelmholtz Equationの近似式を導いた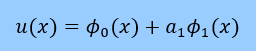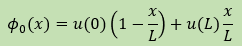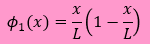

BACK Weighted Residual Method
Menu View Helm wrm Lin Element Rmrk Vari Para Non-L Wire
Internet College of Finite Element Method