One Dimensional Finite Element Method
Weighted Residual Method-9
■左端Dirichlet境界-右端Neumann境界問題および右端が対称条件問題■
これまでは両境界がDirichletの場合を勉強してきました。
左端がDirichletで右端がNeumannの場合、近似式と重み関数はどうなるのでしょうか。
一例として、部材および部材の変形が、左右対称の場合です。
問題 WRM-5の第8と第9番を参考にして下さい。
対称になっている境界がNeumann型境界です。
第8番の問題では、積分範囲を0から1.0としていますが、第9番では0から0.5になっています。結果は、同じになったはずです。
近似式はこれまで通りの下の式で表すことにします。
φ0(x)で境界条件のみを管理し、
φ1(x)でα2のみに対応するようにします。
u(x)=φ0(x)+a1φ1(x)
Neumann型境界条件とは
Neumann型境界ではu(x)の微分値を指定します。例えば左境界がDirichlet型でu(0)が指定され、
右境界がNeumann型でdu(L)/dx=Sが指定されている場合を考えます。
ここの問題でも近似式のφ0が境界条件のみを管理しますので、
下図ではdφ0(L)/dx=Sとなっています。
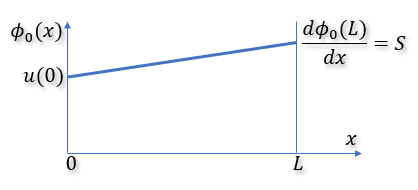
このような問題の場合の近似式と重み関数と積分式はどうなるのでしょうね。
近似式のφ0は上の図のグラフを式にすれば良いので、
φ0(x)=u(0)+Sxで表せられますね。つまり境界条件のみが盛り込まれています。
確かに、φ0(0)=u(0)、dφ0(L)/dx=Sになります。
近似式はなるべく形状関数のN1とN2で表すときれいに書けますので、
φ0(x)=u(0)+LSN2
としておきます。ここに、N2=x/Lです。
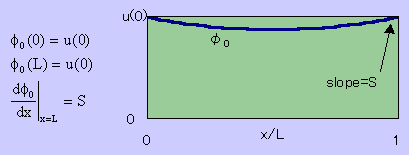
φ0として以下の式を使っても同じ近似解を得ることが出来ます。
φ0(x)=u(0)-LSN1N2
ここに、N1=1-x/Lです。グラフにすると以下になります。
φ0(0)=u(0)、dφ0(L)/dx=Sは守られていますね。
BACK
NEXT
Menu
View
Helm
wrm
Lin
Element
Rmrk
Vari
Para
Non-L
Wire
Internet College of Finite Element Method


