
近似式のφ1はどうなるか。
まず左端はDirichlet型ですのでφ1(0)=0ですね。
右端のNeumann型境界でφ1(L)をxで微分してゼロ以外の値が得られれば
境界値のdu/dxが変わることになるので、
dφ1(L)/dx=0でなくてはなりません。
そして
φ1(x)は微分方程式のα2の変化が反映されなければなりません。
これはNeumann型が与えられている境界点にも適用されなければなりません。つまり、α2が大きくなればu(L)の値も大きくならなければなりません。
よってφ1(L)はゼロ以外でなければなりません。
ですので、ここではφ1(L)=1にしておきます。

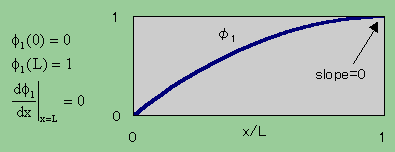
重み関数はGalerkin's Methodによりφ(x)=φ1(x)とします。
積分式はどうなるかです。まず下は重み付け残差法で得られた当初の式です。
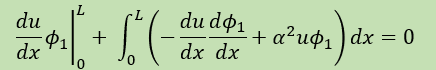
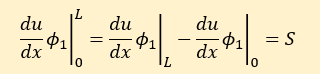
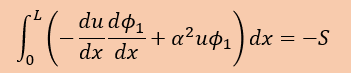
ここで紹介した近似式はちょっと複雑ですので手計算は無し、プログラムを作ってみたのでそれらに沿って計算結果を紹介します。 プログラムの名前は、WRM1X1S1.FORと WRM1X1S.FORです。
プログラム名とφ0(x)の関係は下表のようになっています。 そして計算結果も同時に表示してあります。計算ですが共通な条件としては、u(0)=1, L=0.5, α2=1です。 表示されている値はx=Lでのu(x)です。
| φ0(x) | プログラム名 | S=0の計算結果 | S=0.5の計算結果 |
|---|---|---|---|
| φ0(x)=u(0)+LSN2 | WRM1X1S1.FOR | 1.1388888888888893 | 1.4105902777777968 |
| φ0(x)=u(0)-LSN1N2 | WRM1X1S.FOR | 1.1388888888888893 | 1.4105902777777968 |
φ0(x)として2つの関数を紹介しましたが、u(L)の計算結果は同じでした。 ここでは自由度n=1のみを紹介しましたが、n=2, 3, 4についても計算しました。 wrmeのページに詳細を述べてあります。見て下さい。
■”変位法”■
上でNeumann型境界条件を取り扱う方法を紹介しましたが、
境界値のSが近似式のφ0(x)と積分式の両方に必要でした。
近似式にDirichlet型境界条件を盛り込むのは簡単ですがNeumann型境界条件を取り入れるのは簡単な例題でも
大変な作業になります。
ほとんどの市販のFEMソフトの場合、近似式はNeumann型境界条件のS=du/dxを満足していません。 積分式がSを満足するようになっています。この様な方法を変位法と呼んでいます。 この方法を使うことによりNeumann型境界条件の取り扱いが非常に簡単になりますが、Neumann型境界での計算精度はちょっと落ちることになります。 手の込んだ近似式を作ることを思うとかなり楽ですね。
近似式にNeumann型境界条件を盛り込む必要がなくなると、領域全体を1つのスムーズな式で表す必要が有りません。 折れ線グラフみたいな近似式を使うことが出来ます。