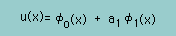
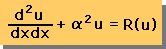
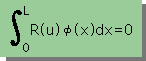
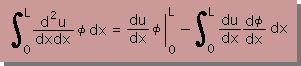
■WRMのまとめ1: 領域を1要素■
ここまでの内容をマスターすると、有限要素法の基礎を理解したとこになります。 この後は、領域を分割した場合の、近似式と重み関数の作り方と、有限要素法の2-3次元への応用です。 勿論、この先には、難問が有りますが、ここまでの内容を理解していれば、スムースに勉強を進められます。 先へ進む前に、いままで勉強した事柄をまとめてみましょう。 つまり、領域を1要素で表した場合です。

WRMの手順

微分方程式に適した近似式を導く(自由度1の場合)。 ここでは、関数φ0が両境界でDirichlet型境界条件を与えているケースを取り上げた。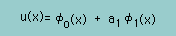
近似式の中に含まれる未知数の数だけ重み関数をGalerkin法で作る。 上の近似式の場合、重み関数はφ1になる。
解析したい微分方程式を L(u)+....=0の形にする。
L(近似式)+....=R(u)とおく。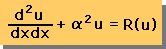
近似式の中に含まれる未知数(Unknown)の数だけの積分式を導く。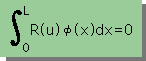
2階微分項は、部分積分で、境界積分と1階微分の領域積分に分離する。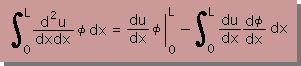
積分式(有限要素式)を導く。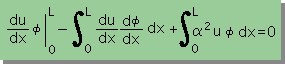
上の式を計算し未知数(a1)を求める。
近似式にa1を代入しu(x)を計算する。

近似式の条件

1. 近似式は、変数*関数の多項式で表わした連続な式であること。
2. 変数は、未知数(Unknown)と同じ単位を持ち、関数は無次元であること。
3. 近似式に用いる関数は、互いに独立関数になっていること。
4. Nuemann 型境界条件が与えられている点において、近似式の値はゼロにならない。

重み関数(φ₁(x))の条件

1. 未知数 a₁の重み関数であるφ₁(x)は、連続でかつ無次元関数であること。
2. 未知数 a₁が支配している領域においてφ₁(x)は有限な値を持ち、領域外(境界)ではゼロになる。 Dirichlet型境界条件が与えられている境界においてφ₁(x)=0でした。
3. Neumann型境界条件が与えられている境界ではa₁の支配領域内であるからφ₁(x)=1 そしてdφ₁(x)/dx=0でした。
4. 自由度が2以上の場合、重み関数は互いに独立関数になっている。

近似式に関し、ここではDirichlet型境界条件とNeumann型境界条件を近似式に埋め込む方法を勉強しました。 しかし実際の場合、どの様な境界条件になるかは与えられた問題によります。 ですから、プログラムミングではどちらの境界条件でも対応できるようにします。