One Dimensional Finite Element Method
Weighted Residual Method-12

■WRMのまとめ2: 近似式u(x)について■
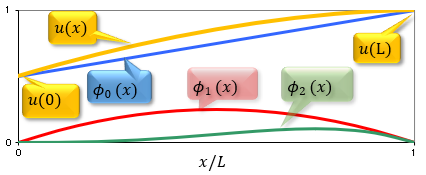
u(x)は左の境界から右の境界まで連続な関数になっていて、その微分であるdu(x)/dxも連続な関数でした。 境界条件は φ0(x)が管理しα2を受け持ち解析の精度に貢献しているのは φ1(x)およびφ2(x)でした。 下図は自由度が2の場合の関数を示します。

自由度を増やすと解析精度が向上します。 下は自由度nの場合の近似式を表します。φi(x)を作るのは大変ですけどね。

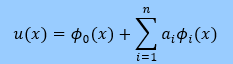
上でも言いましたが、これまでに紹介してきた近似式u(x)は領域全体で連続になっています。 これは連続体の解析においては最低限必要な条件です。 更にu(x)の微分du/dxも領域全体で連続になっています。 このためにNeumann型境界条件を φ0(x)と φ1(x)に盛り込む事が可能でした。 しかし、 φ0(x)と φ1(x)を見つけるのは 大変な作業だったのはNeumann型境界条件の例題をみれば分かります。

近似式u(x)の導出の次のステップとして、u(x)の領域全体での連続性はキープするが微分du/dxは不連続にするという考えです。 Neumann型境界条件を近似式に取り込めないが、近似式u(x)の導出をマニュアル化できます。

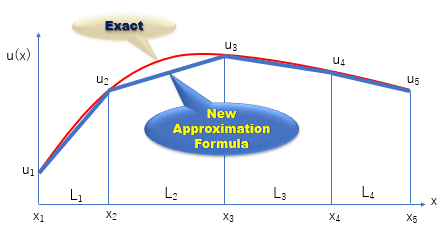
新しい近似式：折線グラフ
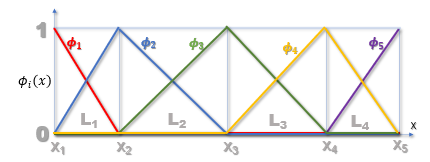
近似式u(x)が下図に示す様な折線グラフで表したら重み付け残差法の手順はどうなるかです。 グラフは4つの直線で表されています。 u(x)は領域全体で連続ですが、微分du/dxは各折れ目で不連続です。

このような場合、近似式u(x)は以下のように書けます。

これまでの近似式とちがうことは以下が上げられる
  1. 得られる計算結果がa1でないく、折れ目でのuiが計算される
  2. φ0(x)が無い
  3. 未知数u1とu5を使いDirichlet型境界条件を挿入できる
  4. Neumann型境界条件は積分式のみが受け持つことになる
  5. 積分式を計算する場合、積分範囲は折れ目から次の折れ目の繰り返しで行う
自由度がnの場合、以下の様にSummationで書くことができます。

ではφi(x)はどんな形をしているのでしょうか。 下図のようになっているのが想像できます。 例えばφ3(x)はx3で1、 x1、x2、x4、x5でゼロになっています。

BACK NEXT
Menu View Helm wrm Lin Element Rmrk Vari Para Non-L Wire
Internet College of Finite Element Method