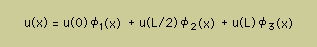
One Dimensional Finite Element Method
Weighted Residual Method-13

■自由度n=3でu(L/2)が得られる近似式■
折線グラフ的な近似式の例題を1つ紹介しておきます。次のLinear Elementに関係が有りますので勉強しておいて下さい。 FORTRANプログラムも用意してありますので、そちらも見て頂ければ有難いです。
まず、直接u(L/2)が得られるように近似式を書いてみました。下の様になります。

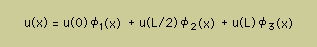
そして、上式の関数 φ1(x), φ2(x), φ3(x) の条件1として、 x=0でu(0)、x=L/2でu(L/2)、x=Lでu(L)が得られる様にするには、下表を満足させなければなりません。 また、下表が満足されれば、どのxでも φ1(x)+ φ2(x)+ φ3(x)=1 でなければなりません。

関数 x=0で x=L/2で x=Lで
φ1 1 0 0
φ2 0 1 0
φ3 0 0 1

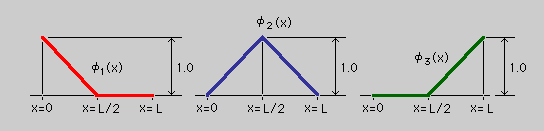
これらの条件を満足する最も簡単な関数 φ1, φ2, φ3 は、 以下の様になります。

上の近似式の場合、未知数(unknowns)は、u1とu2とu3ですね。 これらは全て、α2=P/(EI) の影響を受けることになります。 したがって、x=LにNeumann型境界条件を与えた場合でも、 u3はα2の影響を受けることになります。

上の関数を使って積分式を計算してみましょう。 以前紹介したプログラムWRM1X1.FORのFUNCTION F0とF1を 修正し上図を再現する様に書き換えました。 プログラムTHIRTN.FORのFUNCTION F0とF1 を見て下さい。 IF文を使って上図を再現しています。プログラムを実行すると、u(0)の値を要求してきますので、 例題(WRM-1) の場合u(0)=0を入力して下さい。 結果ファイルとしてTHIRTN.FEMを出力します。 結果を見ると、a1=0.5681818182でu(x=0.5)も同じになっていますよね。

話しはうまく行っている様に思えますよね。 しかし、ここで問題になるのが du/dx です。 上図の関数は折線グラフの様になっていますのでu(x)も連続な関数です。 しかし、du/dxは棒グラフの様になり、x/L＝0.5で不連続になってしまいます。 この不連続が誤差につながっています。 つまり、これが有限要素法の"変位法"です。 では、どうすれば上の不連続性は軽減または消滅させることができるでしょうか。 方法として下の3つが考えられます。

方　法 説　明 結　果
細分割もっと屈折の数の多い折線グラフにする du/dxは滑らかな棒グラフになる
高次関数du/dx が曲線で近似される du/dxも連続に近づく
Hermite関数法u(x) だけでなくdu/dxも未知数とする u(x)もdu/dxも連続になる

上のどの方法も収束性は確認されています。上の3つの方法で最も精度が良いのがHermite関数法です。 しかし、この方法の欠点は未知数が多くなることです。当初、脚光をあびましたが現在では姿をみません。 現在残っている方法は細分割と高次関数の組み合わせです。 次の、1次要素では領域を細分割による方法でHelmholtz equationを解く方法を学びます。

質問/回答
BACK NEXT
Menu View Helm wrm Lin Element Rmrk Vari Para Non-L Wire
Internet College of Finite Element Method