One Dimensional Finite Element Method
Weighted Residual Method-8
■WRM1X1.FOR の簡単な説明■
- プログラムで使われている実数は、全て Double です。
- 積分式の数値計算には、Gauss-Legendre積分のSammpling点数(N=3)を用いています。
- α2=1 としてあります。
- 積分の下限値(XST=0.)と積分の上限値(XEN=1.0)を用います。
- 積分範囲は、幾つかのサブ領域に分割して、積分計算精度を上げています。
分割数(NSEG)は、100としてあります。
- 微分の精度を向上させる1つの手段として、できるだけ小さなΔxを用いる方法がある。
ここでは、DELTAX(Δx)として、サブ領域の長さの1/(MULTI=10)としてあります。
さらに数値微分には
Numericalで説明した中心差分を用いています。
- 近似式はF0(X)+A1*F1(X) としています。
F0(X)=X, F1(X)=X*(1-X) である。F0(X)を変更すると様々なDirichlet境界条件に対応させることが出来ます。
プログラムの計算手順は、下図の様になっています。
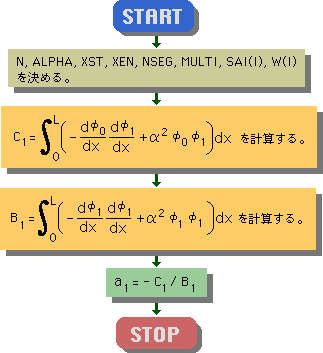 フローチャートの最後のボックスで未知数 a1 が計算されています。
フローチャートの最後のボックスで未知数 a1 が計算されています。
 問題
問題
BACK
NEXT
Menu
View
Helm
wrm
Lin
Element
Rmrk
Vari
Para
Non-L
Wire
Internet College of Finite Element Method


 問題
問題