Numerical Method & Algebla
derivative-2
次に定数 a を決定するには 多少面倒な条件をクリアーしなくてはなりません。
それらの条件を下表に示します。
| 番号 | 定数aの条件 | 定数aの値 |
|---|
| 1 | f(x)=一定(constant)のとき | 0 |
|---|
| 2 | f(x)=線形(linear)のとき | 0 |
|---|
| 3 | f(x)=∪(Cone Cave Up)のとき | + |
|---|
| 4 | f(x)=∩(Cone Cave Down)のとき | - |
|---|
すると上の条件とd2f/dx2=2aを満足するaは次式の様になる。
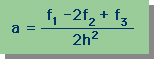 つづいて、定数 b は、a と c が既に分かっているので f(x3) = f3 より求めることが出来ます。
さらに、f(x)= 一定のとき、b=0 に成ることに注意して下さい。
すると b は次の様になります。
つづいて、定数 b は、a と c が既に分かっているので f(x3) = f3 より求めることが出来ます。
さらに、f(x)= 一定のとき、b=0 に成ることに注意して下さい。
すると b は次の様になります。
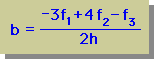 f(x) が f1, f2, f3, と h の関数として得られたので、
df(x)/dx を x=x2 で求めると次の様になります。
f(x) が f1, f2, f3, と h の関数として得られたので、
df(x)/dx を x=x2 で求めると次の様になります。
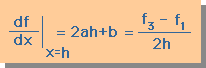 これをhの2次精度の中心差分といいます。
貴方も上の式が正しいか否か確認してみて下さい。
注意しなくてはならない点は関数 f(x) が定数から2次式の範囲であるときに上の式はExactになる。
関数がそれら以外の場合には上式に誤差が含まれることになる。
この誤差を小さくするには、式中の h を小さくします。
これをhの2次精度の中心差分といいます。
貴方も上の式が正しいか否か確認してみて下さい。
注意しなくてはならない点は関数 f(x) が定数から2次式の範囲であるときに上の式はExactになる。
関数がそれら以外の場合には上式に誤差が含まれることになる。
この誤差を小さくするには、式中の h を小さくします。
このサイトで取り上げている要素の形状関数は2次以下ですので形状関数の微分の計算からの誤差は発生しません。
しかし2次元、3次元の要素になると形状関数は2次以上になるので、その場合は以下の4次精度の中心差分を使います。
\begin{eqnarray}
\frac{d f}{d x}=\frac{-f_{i+2}+8f_{i+1}-8f_{i-1}+f_{i-1}}{12\Delta x}
\end{eqnarray}
有限要素法で差分を使うことは形状関数の微分以外に無いので微分については、これぐらいにしておきます。
 内容について疑問および質問がある場合は左のQ&Aボタンを押して下さい。
内容について疑問および質問がある場合は左のQ&Aボタンを押して下さい。
BACK
Matrix
Menu
Integral
Derivative
Matrix
Simultaneous
Internet College of Finite Element Method
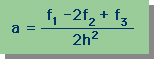
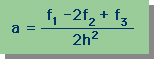
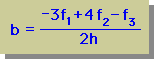
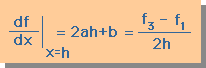
 内容について疑問および質問がある場合は左のQ&Aボタンを押して下さい。
内容について疑問および質問がある場合は左のQ&Aボタンを押して下さい。