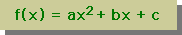■FEMでの微分の計算■
ここでは最も簡単で精度の良い関数の1階微分の数値計算方法を紹介します。
差分法では微分の計算方法が解析の全てを支配していますが、有限要素法のプログラムで数値微分(差分)を行うことは、めったにありません。 皆無といっていいでしょう。 かといって有限要素法において微分の計算がないわけではありません。 実をいうとFEMのプログラムは微分と積分のかたまりのようなものです。 しかし微分の計算の殆どはマトリックス演算の中に隠れています。 ただプログラムの中で目で確認できる微分といえば形状関数の導関数(微分のこと)です。

市販のプログラムでは、あらかじめ手で形状関数(Shape Functions)の導関数を求めておいてプログラムの中で微分を導関数から求めます。
例えば形状関数が f(x)=x² である場合、導関数は f'(x)=2x になります。 つまり x=0.5 でのf(x)の微分値は 1 になります。
しかし、この場合、形状関数はFEMで最重要品目ですから導関数を求める手計算に間違いがあるとプログラム中の全てのプロセスに影響します。 つまり間違った結果を出力することになります。

■2次式の微分■
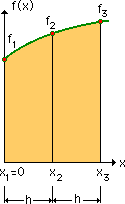
では、どのようにすれば微分が計算できるか考えてみましょう。 下の左図を見て下さい。 図の曲線上の3点を通過させるためにはf(x)を最低2次式にする必要がある。 下の右図がその式になります。
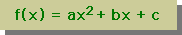