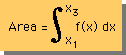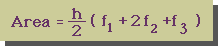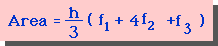integral

Numerical Method & Algebla
Integral-1

有限要素法(FEM)のプログラムでは1つのジョブで数値積分を含むモジュールおよびファンクションが数万回コールされます。特に支配方程式が時間依存ともなると、その回数は膨大になります。したがって効率的かつ精度の高い数値積分法が望まれます。

■従来の数値積分法■
学校の教科書でよく現われるのが、台形則とSimpson則です。貴方の記憶ではSimpson則の方が精度が高いと教わったはずです。確かにそうです。

一般に関数f(x)を機械的に積分する場合、まず全積分範囲を下の図の様な単位に分割します。そして、単位ごとに面積を計算し、それらの合計を計算することにより全面積が得られます。ここでは下図に示す様に2h幅を単位とした面積の計算方法について説明します。

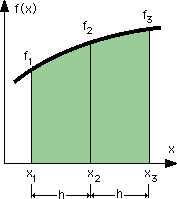
上図で、f(x)が、積分される関数です。図中の x₁、x₂、x₃はサンプリングポイント(sampling points)と呼ばれています。そして緑に着色されている部分が求めようとしている面積です。つまり下式です。

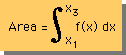f(x)が線形だと台形則による数値解は厳密解と同じになります。 Simpson則では、それ以上の精度をだすことが可能になります。余談ですが、Simpson則は、タンカー(原油輸送船)の体積を求めるために使われていました。当時、船の設計に携わっていた人々をSimpson屋と呼んでいたそうです。

台形則で着色してある部分の面積を計算すると次の様になります。

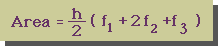Simpson則で同様に面積を計算すると、次の様になります。

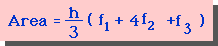上の式はSimpson則の中で最もシンプルで一番よく目にする式です。この場合f(x)が二次曲線まで数値解は厳密解と同じになります。