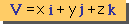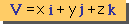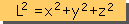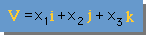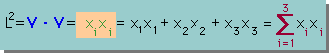Numerical Method & Algebla
Matrix
有限要素法のプログラムを開発する上で、ベクトル(Vector)、テンソル(Tensor)、マトリックス(Matrix)演算規則の知識は、不可欠です。
Vectorは領域の境界面の計算処理に、Tensorは支配方程式(Governing Equation)を立てるときにMatrixは、支配方程式の離散化(Discretization)のときの使われます。
これらは、有限要素法を学ぶ上で必ず使う道具ですので納得の行くまで勉強してください。
■Vectorの長さ■
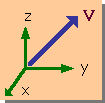
手始めにVectorの長さを計算してみよう。下の左図のVectorを、下の右図の式の様に定義します。
殆どの数学の本も、これと同じ定義を使っています。
Vectorの表示方法として、最初は、文字の上に矢印を書いていました(今でも使っている)。
この方法は、印刷技術の乏しい当時としては、大変苦労する表示方法だったそうです。
そこで印刷が簡単な 太文字を使う方法が考えだされたそうですよ。
さてVectorの長さ(L)は、Vectorの内積(Dot Product)で求まります。
つまり、L2=V・Vとなる。
これを展開すると次の様になります。
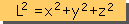 VectorはTensorでも表わすことが出来ます。
まず上図の座標 x, y, z を下図に示すように、x1, x2, x3 で書き改めます。
VectorはTensorでも表わすことが出来ます。
まず上図の座標 x, y, z を下図に示すように、x1, x2, x3 で書き改めます。
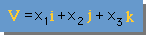 次にTensor表示法のルールに従いVectorの長さを計算すると下の様になります。
次にTensor表示法のルールに従いVectorの長さを計算すると下の様になります。
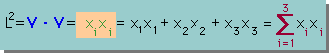
ここに添え字の i を Index をいいます。
上式の場合1つの項に同じ添え字が2つ存在しています。
ルールでは加算されることになっています。
結果がスカラー(Scalar)になります。
この場合の添え字の i を、 dummy index といいます。
この様に、数式をTensorで書くと、加算を意味するギリシャ文字のΣを省くことができます。
つまり、数式をコンパクトに書くことができます。
Tensor表示法について2次元FEMの紹介の時にもう一度詳しく触れます。
BACK to Derivative
NEXT
Menu
Integral
Derivative
Matrix
Simultaneous
Internet College of Finite Element Method