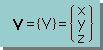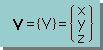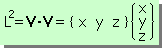Numerical Method & Algebla
Matrix-2
さて、VectorをMatrix表示法で書くと、どうなるかを考えてみよう。
Matrix表示法では、Vectorに {V} を、Matrix に [M] を使います。
よって、Vector V は、次の様に書けます。
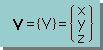 さて、Matrix表示法のルールを用いると、Vectorの長さはどの様に書けるか考えてみよう。
Matrixの演算方法に従うと、Vectorの長さは次の様に書けます。
さて、Matrix表示法のルールを用いると、Vectorの長さはどの様に書けるか考えてみよう。
Matrixの演算方法に従うと、Vectorの長さは次の様に書けます。
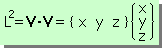 さらに、Matrix表示法では、{ x y z }={V}Tですから2つのベクトルの内積は、次式の様にコンパクトになります。
ここにTをトランスポーズ(Transpose)と呼ばれています。
さらに、Matrix表示法では、{ x y z }={V}Tですから2つのベクトルの内積は、次式の様にコンパクトになります。
ここにTをトランスポーズ(Transpose)と呼ばれています。

以上Vectorの長さを求める3つの方法(index, vector, matrix)を紹介しました。
有限要素法では数式展開の過程で支配方程式を”エネルギー”の量に変換します。
つまりエネルギーはScalarであり弾性解析の場合、F・dで計算されます。
ベクトルの内積、つまりVectorの長さ( or エネルギー)を求める方法の理解は有限要素法において重要なステップの1つになっています。
BACK
NEXT
Menu
Integral
Derivative
Matrix
Simultaneous
Internet College of Finite Element Method