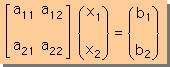
ここでは、連立方程式を機械的に解く方法で、最も広く使われているGaussの消去法を紹介します。 この部分を理解するのに、高等な学力は必要ありません。 精々、中学レベルで十分です。 しかし、連立方程式の解き方は、有限要素法での解析精度に大きな影響を与えますので、計算結果に含まれる誤差については、しっかりと勉強する必要があります。 また、計算効率も、有限要素法のプログラミングでは、重要なファクターの1つです。
このセックションでは、有限要素法でのプログラミングでよく使われる、 4つの型のGaussの消去法を紹介します。 しかし、市販されているソフトでは、もっと安定度が高く計算効率の良いGaussの消去法が使われています。 それらについては、書物を参考にして下さい。■FEMにおける連立方程式の解法の概要■
有限要素法では、微分方程式を離散化し連立方程式を作ります。
つまり、[K]{u}={RHS}です。その連立方程式に境界条件を埋め込み未知数(unknowns {u}) について解きます。
■2X2の連立方程式■
前置きはこれぐらいにして、とりあえず、マトリックスが
2X2の連立方程式の解法から始めたいと思います。
下に示す連立方程式を解いてみよう。
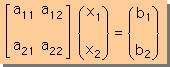
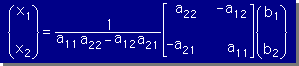
この方法で連立方程式を解く場合 [A]の逆行列は [A]-1=[adj[A]]/det[A]で機械的に計算できます。
その他に 有名な方法として”Kramer's rule”が有ります。
これは、行列値の比で{X}を求める方法です。
しかし これらの方法は、残念ながら効率的に連立方程式を解く方法ではありません。
精々 3X3の連立方程式が限度です。
それ以上になると掛け算と割り算の数がGaussの消去法に比べ多くなり、有限要素法のプログラムには不向きです。