1X3 の Matrixの例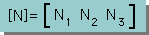 |
3X2 の Matrixの例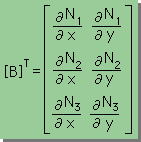 |
|---|---|
2X3 の Matrixの例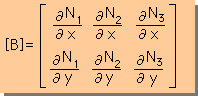 |
|
| 3X3 の Matrixの例 [B]T[B]= 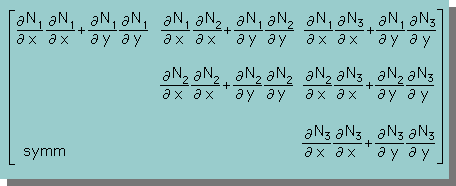 |
|
■Matrixの特徴■
Matrixについて簡単に触れておきます。Matrixは、[A]で表わし、大きさを2X3の様に数字で表現します。
下は、三角形要素を用い、有限要素法のプログラムを作るときに、よく使われるMatrixです。
1X3 の Matrixの例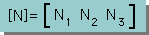 |
3X2 の Matrixの例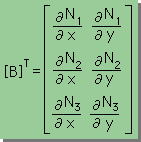 |
|---|---|
2X3 の Matrixの例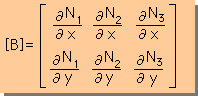 |
|
| 3X3 の Matrixの例 [B]T[B]= 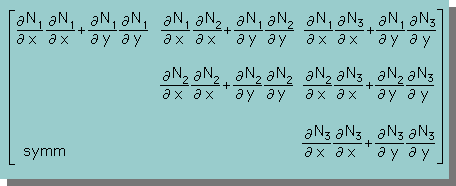 |
|
次にMatrixの加減乗除について簡単にふれておきます。
| Matrixの加減算を行う場合、2つのマトリックスの大きさは同じでなくてはならない。 |
| Matrixの乗算が施される、2つのマトリックスの大きさには、決まりがあります。 [A][B]を行う場合、Matrix [A]がnXmであれば、Matrix [B]はmXnでなくてはならない。 結果は、nXnになる。上の3X3 の Matrixを参考にしてください。 |
| Matrixの除算が施されるマトリックスの大きさにはnxnの正方でなくてはならない。 [A]{X}={C}を例にとると、{X}をユニークに求めるために[A]は正方でなくてはならない。 そして、{X}は、[A]-1{C}で求まる。ここに、[A]-1を[A]のInverse(インバース)と言う。 |