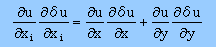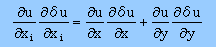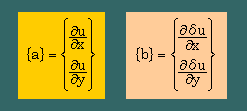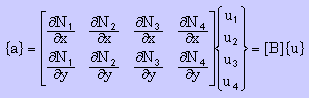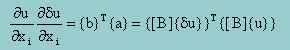matrix4

Numerical Method & Algebla
Matrix-4

■MatrixとVectorの演算■
有限要素法では、式を導いている過程で、下に示す様な結果がスカラーになる計算が頻繁にでてきます。下式は、2次元のケースです。そして、これをマトリックス演算方式で表し、視覚的に覚え易いマトリックス演算に書き換えます。

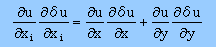最終的に連立方程式を組み立てて、未知数を得ています。したがって、有限要素法では、マトリックス演算は必須になります。早速、勉強にかかりましょう。まず、マトリックス形式で、2つの物を掛算してスカラーが得られるのは、どういう物でしょうか。スカラーを得るには、ベクトル掛けるベクトルが必要になります。つまり、２つのベクトルのDot Productですね。マトリックス形式では、以下の様に書きます。

Scalar={a}^T{b}

ここに、{a}と{b}は、ベクトルです。上付きのTは、トランスポーズ(転置)を意味します。上のその上の式の場合、{a}と{b}は、以下の様に書けます。

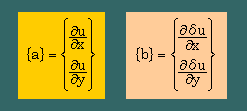結果がスカラーですから、{b}^T{a}と書いてもOKですね。ここでは、{b}^T{a}を使います。さらに、有限要素法では、要素の形状関数を使って、{a}と{b}を近似します。例えば、以下の様に近似されたとします。 2次元の4節点要素を仮定しています。

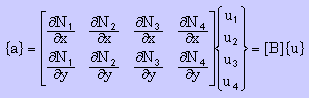
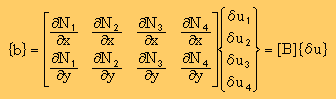すると、{b}^T{a}は、マトリックス表記法を用いると、以下の様になります。

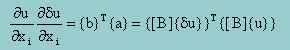
BACK NEXT

Menu Integral Derivative Matrix Simultaneous Internet College of Finite Element Method