■Gauss-Legendre法■
数値積分の精度を向上させるにはf(x)の特徴をよく理解している法則を使い分割幅(h) を可能な限り小さくすることです。
ここで問題になってくるのが解析精度とサンプリングポイントの数のバランスです。
つまり数値積分の計算に必要とされる掛け算と割り算が少なくて解析精度の高い数値積分方法が望ましいことになります。
その様な厳しい条件に応えてくれるのが有限要素法で最もよく使われているGauss-Legendre法です。
この方法を用いるとSimpson則に比べ少ないサンプリングポイントで、より高い計算精度が得られます。
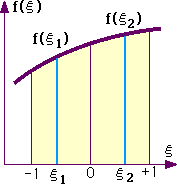
まず、この方法の使い方を2-Point法と下図を用いて説明します。
下図の横軸は無次元座標のξです。縦軸がf(ξ)です。

すると上図の塗りつぶした部分の面積はGauss-Legendre法によると次の式で計算できます。

ここでξi(上図の水色の線)はSampling pointでの座標値でwiはWeighting factorです。 そして、それらの値は下表のようになっています。
| Two-Point Gauss-Legendre Quadrature | ||
| i | ξi | wi |
|---|---|---|
| 1 | -0.577350 | 1.000000 |
| 2 | +0.577350 | 1.000000 |
ここで一言:積分の計算誤差が最小になるように上表の ξiとwi の値を決めています。 このGauss-Legendre法の特徴としてはξiおよびwiが左右対称になっています。 つまり、Σwi=2、Σξi=0 になっています。 ξiおよびwiの値の計算方法については文献を参照して下さい。