integral

Numerical Method & Algebla
Integral-4

■例題 ∫₀^{^π/2}sin(x)dx■
それでは早速 2-Point Gauss-Legendre Quadrature を使って sin(x)を 0 から π/2 まで積分してみましょう。下図に示すように積分領域を2分してあります。

領域1の長さは1.0で、領域2は0.5708です。各々の領域に対し2-Point Gauss-Legendre を適用します。計算手順と結果を下表にまとめてありますので、貴方も電卓で計算してみて下さい。出来れば 3分割、4分割で計算して、どのように精度が向上するかを観察するのも良いでしょう。

わりと荒っぽい領域の分割ですが、計算結果は厳密解(1.0)に近い値になっています。

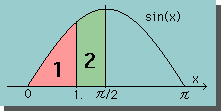
最後に座標変換の式について触れておきます。通常、座標変換式は無次元座標のξ(Gauss座標とも言う)をベースにした形状関数を使うと簡単に得られます。例えば線形1次要素の場合、次の様になります。これらは1dimで出てくる形状関数とは、ちょっとちがいますので注意して下さいね。

\begin{eqnarray} N_1=\frac{1}{2} \left(1-\xi\right) \end{eqnarray}

\begin{eqnarray} N_2=\frac{1}{2} \left(1+\xi\right) \end{eqnarray}

すると変換式は下の様に書けます。 \begin{eqnarray} x=N_1 x_1+N_2 x_2 \end{eqnarray} すると前に紹介した下の変換式が得られます。

この様に形状関数が作成できれば変換式も簡単に得られます。形状関数については今後1dimや Parametric Elementsで出てきますので、そこで勉強して下さい。ここではGauss-Legengre法を使って積分が出来ればOKです。

内容について疑問および質問がある場合は、左のQ&Aボタンを押して下さい。