■変換例: xy座標系から極座標系へ■
それでは、 が正しいかどうか、再度、別の角度から確認してみましょう。確認の方法として、ここでは、Jacobian Matrix を、xy座標系から極座標系へ変換してみます。つまり、dxdyがrdrdθになるかどうかを確かめてみると言うことです。要するに、下の積分の変換ですね。
が正しいかどうか、再度、別の角度から確認してみましょう。確認の方法として、ここでは、Jacobian Matrix を、xy座標系から極座標系へ変換してみます。つまり、dxdyがrdrdθになるかどうかを確かめてみると言うことです。要するに、下の積分の変換ですね。

x=rcosθそして、y=rsinθですから、Jacobian Matrixは、次の様になります。
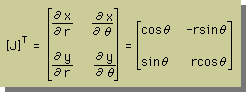
Jacobian Matrixの行列値(Determinant)を計算すると、次の様に結果は半径 r になります。
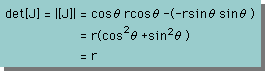
よって、dxdyは、 で置き換えられることが確認されました。
で置き換えられることが確認されました。
したがって、xy座標系のdxdyは、 で置き換えられることは、正しいと言えます。座標変換について、詳しく知りたい方は、解析学等の本を参考にして下さい。
で置き換えられることは、正しいと言えます。座標変換について、詳しく知りたい方は、解析学等の本を参考にして下さい。
以上をまとめると、関数 f(x,y) を、Gauss-Legengre法を考慮した無次元座標系で積分すると、下式の様になります。
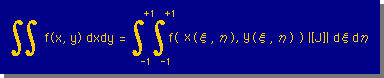
これで、[N]T[N]の積分は、可能になりましたね。しかし、まだ、[B]T[B]の積分が残っていますよ。
■形状関数の微分■
積分の次は、微分です。ここで紹介している 4-Nodedの形状関数は、無次元座標系で書かれていますので、形状関数を無次元座標系の従属変数で微分することは簡単です。しかし、実座標系の従属変数(x, y)で形状関数を微分することは、ちょっと難しいですよ。
1次元では、どの様に微分していたか思い出して下さい。1次元の実座標系での形状関数は、xのみの関数ですから、形状関数Niの全微分は、dNi=(dNi/dx)dxです。よって、dNi/dξ=(dNi/dx)dx/dξとなります。
2次元の実座標系での形状関数は、xとyの関数であるから、形状関数Niの全微分は、次の様になります。
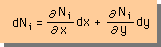
つまり、dNi(x,y)は、Niのx方向の変化とy方向の変化の合計であると言うことを意味しています。 さらに、上の式の両辺を無次元座標系の従属変数(ξとη)で微分すると、下式の様になります。
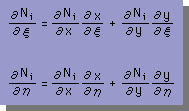
上の式をもっと見易くするために、マトリックス表示法で書いてみましょう。下の様になります。
 |
または、 | 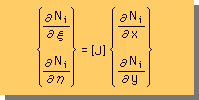 |
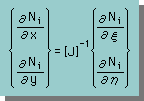
2X2マトリクッスの逆行列は、わりと簡単に計算できます。下式を見て下さい。
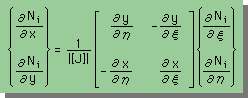
貴方は、上の逆行列が正しいかどうか、確認して下さいね。2X2の連立方程式の計算方法は、 以前、勉強しましたよね。
| BACK | NEXT |
|---|
| Menu | 4-noded | Create | 8-noded | 9-noded | 12-noded | 3-Dim | Example | Helmholtz |