■概要■
これまでは、4-noded Iso-parametric 要素を用いて、話しを進めてきました。しかし、解析のタイプによっては、より高い精度を要求される場合があります。したがって、解析の用途に適した要素(2次要素等)が使えるようにするためには、形状関数の作り方を勉強する必要があります。
ここでは、形状関数を簡単に作る方法を紹介します。
■4-Nodedの場合の形状関数の作り方■
手始めに、4-Nodedの形状関数を作ってみましょう。まず、f(ξ, η)=0 になる関数で、節点を通過する直線を用意します。下図を見て下さい。
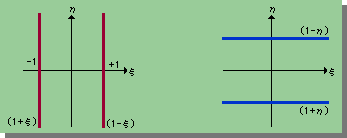
4-Noded 要素では、下図の節点番号1の形状関数(N1(ξ, η))を作るためには、節点番号の2と3と4でN1(ξ, η)がゼロになる様にする必要があります。
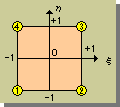
つまり、節点番号の2から3と3から4の境界上でゼロになる関数を作ればよいことになります。したがって、上図を参考にすると、N1は、次の様になります。
| N1(ξ, η)=a(1-ξ)(1-η) |
そして、節点番号1で、N1(ξ, η)=1になる様に定数aを調整すればよいことになります。この場合、a=1/4です。同様にして、N2(ξ, η), N3(ξ, η), N4(ξ, η)も作ることができる。 そして、最後にN1+N2+N3+N4=1になることを確認すればよいのです。
| BACK to 4-noded Element | NEXT |
|---|
| Menu | 4-noded | Create | 8-noded | 9-noded | 12-noded | 3-Dim | Example | Helmholtz |