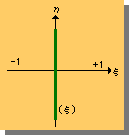Parametric Elements
Parametric Elements
Create Elements-2

■6-Nodedの場合の形状関数の作り方■
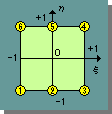
下図に6-Nodedの要素を示します。4つの境界線の2つが直線(節点1-6と 3-4の間)で、他の2つが2次曲線(節点1-2-3と 6-5-4の間)まで対応できる要素になっています。したがって、実座標系では、領域の境界をに1次と2次曲線で描くことが出来ます。
6-Nodedの場合、上図の右の様に、節点番号2と5を通過し、値がゼロになる関数が必要になってきます。
では、早速、形状関数を作ってみます。まず、N1(ξ, η)から考えてみましょう。この場合、節点番号2と3と4と5と6で、N1(ξ, η)がゼロにならなくてはなりません。したがって、
形状関数のN2(ξ, η)は、どうなるでしょう。節点番号1と3と4と5と6で、N2(ξ, η)がゼロにならなくてはならないので、次の様になります。
| N2(ξ, η)=b(1+ξ)(1-ξ)(1-η) |
貴方は、上の式が正しいかどうか確認して下さい。
同様に、N3、N4、N5、N6についても式を作ります。そして、Ni(ξj, ηj)=δij になるように定数a, b, ....を調整します。さらに、N1+N2+N3+N4+N5+N6=1 になることを確認します。