■Wave Equation■
2-Dim Helmholtz Equationに入る前に、Wave Equationについて簡単に触れておきます。2次元の膜振動などを表わすWave Equationは、次の様に書くことが出来ます。

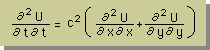
ここに、c²は、膜の張力を膜の密度で割った値を示します。uは、膜の変位を示します。

Wave Equationの解であるWave functions U(x,y,t)は、時間軸方向に関し”調和関数”(Harmonic functions)になっています。よって、Wave Equationの解を、次式で書き表すことができます。

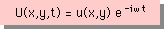
ここに、ω=Wave frequency、i²=-1です。Wave Equationの詳細については、 Referencesを参考にして下さい。

上の解をWave Equationに代入すると、2次元Helmholtz equation が出来上がります。下式がそうです。式中のα=ω/c です。

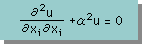
■2-Dim Helmholtz Equation有限要素式■
Helmholtz Equationの有限要素式については、1次元で詳細を述べましたので、ここでは結果のみを紹介します。1次元の式の領域積分を2次元積分に、そして境界積分を1次元積分にすると、下の2-Dim Helmholtz Equationの 積分式が出来上がります。

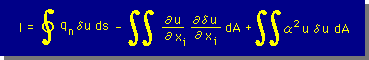
ここに、q_n=∂u/∂n です。

そして、マトリクッス型積分式は、次の様になります。

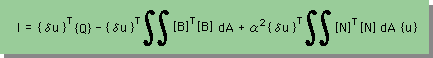
計算機で解くことの出来る有限要素式は、∂I/∂{δu}^T=0で得ることができます。