もう自分の力で要素の形状関数を作れそうですか?。Parametric Elementsの1つとして、3次元要素の作り方を紹介しておきます。その前に、要素の作り方について復習しておきましょうね。下に2次元の場合の条件を示します。
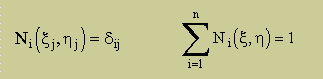
ここに、nは要素の節点数の数を意味します。つまり、形状関数の数ですね。
3次元ではどうでしょうか?。まったく同じですね。ただ、次元が2から3になっただけです。つまり、要素の条件式は、次の様になります。
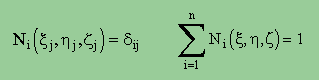
では、”どうやって形状関数を作るか”です。これまでにやってきたことを思い出して下さい。形状関数を作る前に、ゼロ関数を準備しましたよね。1次元要素の場合は、点でゼロになる関数を作りました。2次元では、線でゼロになる関数を準備しました。
そうです。3次元では、面でゼロになる関数が必要になりますね。下図を見て下さい。3次元で代表的な要素です。6面体1次要素と呼ばれています。節点数は、8つですから、形状関数も8つ必要ですね。
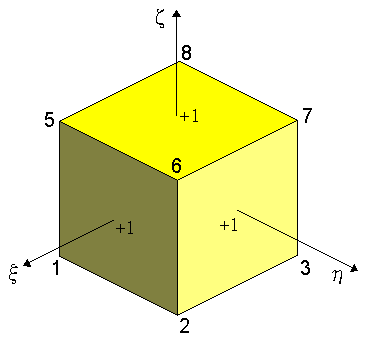
そこで、ξが+1の面でゼロになる関数は、(1-ξ) ですね。では、ηが+1の面でゼロになる関数は何ですか?。(1-η)ですね。つづいて、ξが -1 の面(見えない面)でゼロになる関数は何ですか?。(1+ξ)ですね。そして、ζが +1 の面でゼロになる関数は何ですか?。(1-ζ)ですね。
すると節点番号1の座標は、(+1,-1,-1)ですから、節点番号1の形状関数は、次の様になりますね。
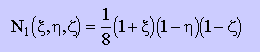
| 12-noded | NEXT |
|---|
| Menu | 4-noded | Create | 8-noded | 9-noded | 12-noded | 3-Dim | Example | Helmholtz |