その他の節点についても同様な作業を行うと、6面体の要素の形状関数が出来上がります。次の様になるでしょう。

節点番号	節点の座標(ξ,η,ζ)	形状関数
1	(+1,-1,-1)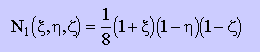
2	(+1,+1,-1)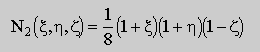
3	(-1,+1,-1)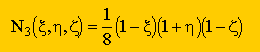
4	(-1,-1,-1)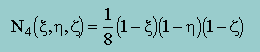
5	(+1,-1,+1)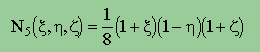
6	(+1,+1,+1)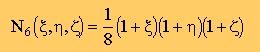
7	(-1,+1,+1)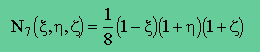
8	(-1,-1,+1)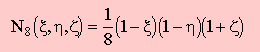

これで要素の作成については、おしまいです。しかし、市販のソフトでは、まだまだ様々な要素が使われています。例えば、Super Parametric要素を使ったP法があります。この方法では、形状関数の次数を上げるために、節点での未知数(unknowns)以外に、1次元の自由度2で紹介したような未知数a₁やa₂が形状関数に add on されてきます。少ない要素数と少ない節点数(n)で解析していますが、Global matrixのサイズは、nXnよりかなり大きくなります。

その他に、Hermite polynomials を使った形状関数があります。この関数は、隣接する要素間の未知数を連続にするだけでなく、未知数の微分も連続にします。ちょっと想像しただけでも、かなり複雑な関数だということが分かりますよね。事実、とても複雑です。 多分、どの市販ソフトでも使われていないと思いますよ。しかし、解析精度は、比べ物にならない位、向上するそうですよ。昔、アリゾナ大学(U of A)にいたときに、授業で1次元の計算例を聞いたことがあります。

要素は、解析精度と解析解の安定性と深い関係にありますから、皆様は、引き続き要素の作成について、勉強して下さいね。

次のExampleでは、三角形要素で使った例題を、4-Nodedと8-Nodedと9-Noded要素で計算します。解析精度と解析解の安定性を学んで下さいね。では。