■Parametric 要素の概要■
現在市販されている有限要素法のソフトの殆どは、Parametric 要素で構成されています。Parametric 要素には、下表の3つに分類できます。
| 要素の型 | 意 味 |
|---|---|
| Super-Parametric | 境界線上の変数を表わす近似式の次数が、要素の境界線を表わす式の次数よりも高い場合を言います。 |
| Iso-Parametric | 境界線上の変数を表わす近似式の次数が、要素の境界線を表わす式の次数と同じ場合を言います。 |
| Sub-Parametric | 境界線上の変数を表わす近似式の次数が、要素の境界線を表わす式の次数より低い場合を言います。 |
ここでは、Iso-Parametric 要素について説明します。理由は、上に示した3つの要素型の中で、プログラミングが一番簡単だからです。なぜ簡単かと言うと、変数用に余分な近似式を作る必要がないからです。
有限要素法を理解する上で、Parametric 要素は、Divergenceの定理の次に難しい存在です。三角形要素から脱皮するためには、避けては通れません。プログラミングもかなり複雑になってきます。さらに、今までは、形状関数の微分と積分を簡単に行えましたが、Iso-Parametric 要素では、座標変換をしながら微分と積分を計算します。
■三角形要素の欠点■
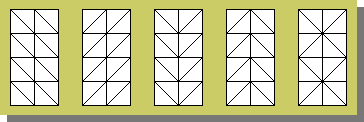
先へ進む前に、三角形要素の欠点と4-Noded Iso-Parametric要素を使う理由を述べておきます。下の図を見て下さい。三角形要素で領域を分割しています。要素の数と節点の数と節点の座標は、全て同じです。しかし、要素分割の方法が異なるため、解析結果に微妙な違いが発生します。この領域を4-Noded Iso-Parametric要素で分割すると、解は1つで、要素数も三角形要素の半分で済みます。
| BACK to Remark | NEXT |
|---|
| Menu | 4-noded | Create | 8-noded | 9-noded | 12-noded | 3-Dim | Example | Helmholtz |