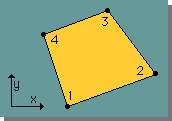
この要素上で温度(T(x,y))を表わすと、節点数が4つですから、次の様になりますね。
| T(x, y) = a + bx + cy + dxy |
つまり、三角形要素よりも1つ節点が多いので、式中の未知数も1つ増えることになります。
上の式の中にxとyの積の項が最高次項であることから、この要素のことを、4-Noded Bilinear Iso-Parametric要素とも言います。
これから、4-Noded Iso-Parametric要素を用いて有限要素式(Matrix型積分式)を導き、連立方程式を立てることになります。そこで、三角形要素で説明した事柄を参考に、何が必要で、どんな計算をするかを思い出して下さい。それらは、以下の項目が必要でしたね。
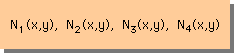
形状関数がxとyで微分できること。
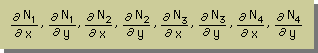
形状関数を積分出来ること。
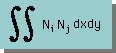
形状関数を1階微分し、積分出来ること。
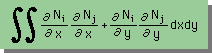
| BACK | NEXT |
|---|
| Menu | 4-noded | Create | 8-noded | 9-noded | 12-noded | 3-Dim | Example | Helmholtz |