前ページの項目の1と2は、なんとか三角形要素のところで学んだTechniqueで出来そうですが、3と4は、気が遠くなりそうな計算が要求されそうですね。そこで、計算手順を単純化するために、座標変換を用います。つまり、x-y座標上の要素をξ-η無次元座標(下図参照)に変換し、前ページの項目1、2、3、4を行います。

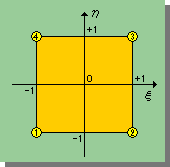
まず、無次元座標上での、形状関数を紹介します。その前に、形状関数の基本ルールを思い出して下さい。以下の様でした。

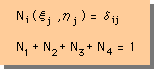
基本ルールに適合した四角形要素の形状関数は、次の様になります。座標軸は、無次元であることに注意して下さい。

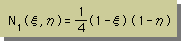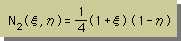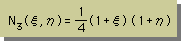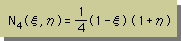すると、温度は、無次元座標上で次の様に書き表すことが出来ます。

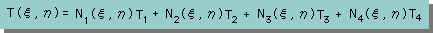
同様に、実座標の独立変数のxとyも、無次元座標系の形状関数で書けます。まとめると、以下の様になります。

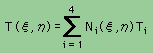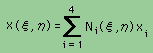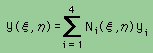ここに、T_i、x_i、y_iは、それぞれ、要素の節点での温度、x座標値、y座標値を示します。