■座標変換■
有限要素式(Matrix型の積分式)を作る上で必要になる材料は、揃いました。次は、関数f(x,y) の積分を行うための、前準備を行います。まず、dxdyとdξdηとの関係を調べてみましょう。下にdxとdyの全微分を示します。
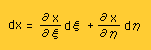 | 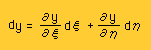 |
|---|
上の式をマトリックス表示法で表わすと、次の様になります。
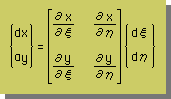
さらに、上の式を、 で表わすことにします。ここに、[J]をJacobian Matrix と言います。
で表わすことにします。ここに、[J]をJacobian Matrix と言います。
この[J]マトリックスは、無次元座標値ξとηが与えられれば、何時でも下式により計算することが出来ます。
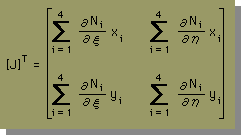
では、関数 f(x,y) の積分は、無次元座標上で、どの様にすれば、計算が出来るのかを考えてみましょう。
1次元の場合は、dx=(dx/dξ)dξより、dx=|[J]|dξで置き換えることが出来ました。2次元でも、
 で置き換えられそうですね。たたし、1次元の[J]は、1つの全微分スカラーですが、2次元になると、[J]は4つの要素を持ち、各々は偏微分で表されています。
注意: |[J]|=[J]の行列値=det[J]
で置き換えられそうですね。たたし、1次元の[J]は、1つの全微分スカラーですが、2次元になると、[J]は4つの要素を持ち、各々は偏微分で表されています。
注意: |[J]|=[J]の行列値=det[J]
■変換 の確認■
の確認■
ここのところは、ちょっと難しいので、ゆっくり行きましょうね。4-Noded Iso-parametric要素は、自由な四辺形になれますが、まず、変形を長方形に限定して座標変換を考えてみましょう。つまり、実座標と無次元座標との間に回転がない状態です。すると、座標変換式は、x=x(ξ), y=y(η) なりますね。また、図で表すと、下の様になります。
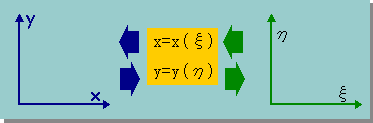
この場合、1次元の座標変換と同じですから、dxとdyは、次の様に書けますね。
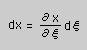 | 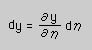 |
|---|
| BACK | NEXT |
|---|
| Menu | 4-noded | Create | 8-noded | 9-noded | 12-noded | 3-Dim | Example | Helmholtz |