前ページの最後の式の右辺を、実座標から見ると、次のベクトルV1とV2で表現することが出来ます。
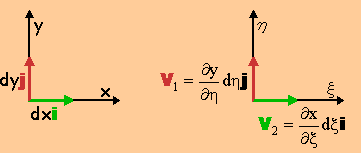
すると、微少面積 dxdy は、ベクトルの積の(V2×V1)・kに該当することになりますよね。つまり、次の様な結果になります。
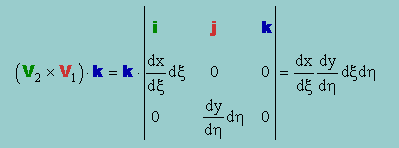
関数 f(x,y)を積分することを考えると、座標軸間に回転がない場合は、下の様な形になります。
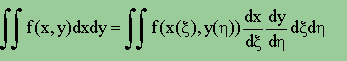
次に、座標間が回転している場合を考えてみましょう。座標値xとyは、x=x(ξ,η), y=y(ξ,η) で表されることになりますよね。すると、dxとdy は、Taylor展開により、前ページで紹介した通り、次の様に書けますね。
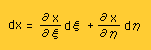 | 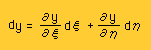 |
|---|
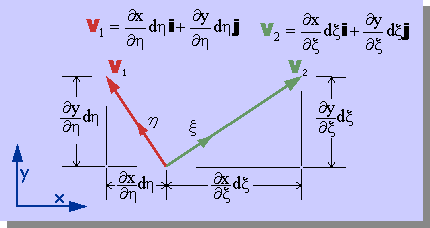
そして、以前と同様に、これらを実座標系から見ると、下図の2つのベクトル V1とV2が現れます。
| BACK | NEXT |
|---|
| Menu | 4-noded | Create | 8-noded | 9-noded | 12-noded | 3-Dim | Example | Helmholtz |