すると、(V2×V1)・kは、下の式で計算出来ましたね。
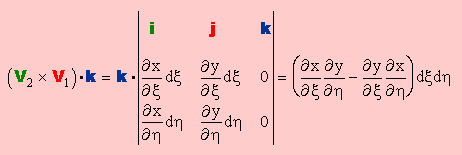
結果を、よーく観察すると、ここで私達が確認しようとしている|[J]|dξdη になっていることに気付くと思います。つまり、実座標での関数 f(x,y)は、下式に示す様に、無次元座標で積分できることになります。
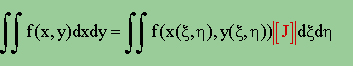
■Divergenceの定理を使った の変換方法■
の変換方法■
Divergenceの定理の副産物として面積の計算方法を前に紹介しました。この方法を使って、変換された無次元座標上での関数f(x,y)の積分式(つまり上の式)の導出を試みてみましょう。まず、閉じた曲線内の面積は、下式で与えられていました。
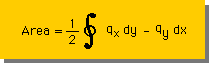
そして、テーラー展開によるdxとdyは、以下の様に書けました。
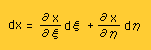 | 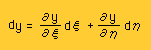 |
|---|
これらを面積の計算式に代入すると、次の様になります。ここまでは、OKですよね。
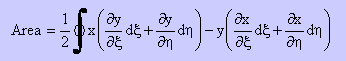
少し整理し、並び替えると、下式の様になる。
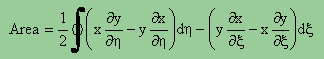
| BACK | NEXT |
|---|
| Menu | 4-noded | Create | 8-noded | 9-noded | 12-noded | 3-Dim | Example | Helmholtz |