先へ進む前に、無次元座標上でのDivergenceの定理を下に書いておきます。実座標上の式となんら変わりはありませんが、シンボルが変わると、頭は簡単についてきませんのでね。
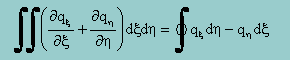
上の式の右辺とAreaの式を見比べ、qξとqηを以下の様に定義してみます。

これらをAreaの式に代入し、Divergenceの定理を適用すると、以下の様に展開できます。ちょっと複雑ですが、貴方もトライしてみて下さい。
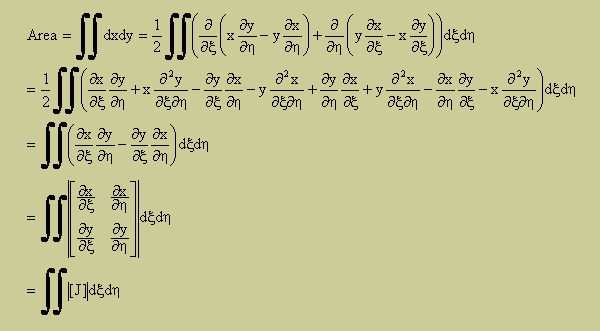
よって、この結果からも、dxdyを|[J]|dξdηで置き換えられることがわかりました。したがって、実座標系でのf(x,y)の積分は、下の式に示す様に、無次元の座標系上で積分できることになります。
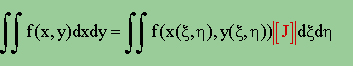
| BACK | NEXT |
|---|
| Menu | 4-noded | Create | 8-noded | 9-noded | 12-noded | 3-Dim | Example | Helmholtz |